Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có 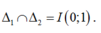
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
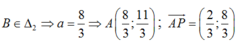
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0

Với \(a\ne0\) ta có:
\(\left\{{}\begin{matrix}-\frac{3}{2a}=-3\\c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\c=4\end{matrix}\right.\) \(\Rightarrow y=\frac{1}{2}x^2+3x+4\)

A B C K P Q M N
Áp dụng ĐL Melelaus có \(\frac{\overline{QB}}{\overline{QC}}.\frac{\overline{MA}}{\overline{MB}}.\frac{\overline{NC}}{\overline{NA}}=1\Rightarrow\frac{\overline{QB}}{\overline{QC}}=\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NA}}{\overline{NC}}\) (1)
Áp dụng ĐL Ceva có \(\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NA}}{\overline{NC}}.\frac{\overline{PC}}{\overline{PB}}=-1\Rightarrow\frac{\overline{PB}}{\overline{PC}}=-\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NC}}{\overline{NA}}\) (2)
Từ (1) và (2) suy ra \(\frac{\overline{PB}}{\overline{PC}}=-\frac{\overline{QB}}{\overline{QC}}\). Như vậy \(\left(BCPQ\right)=-1\)tức là hàng điều hòa (đpcm).
P/S: Đề bị thừa điểm O nhé bạn.
Cho mình sửa dòng thứ hai: \(\frac{\overline{PB}}{\overline{PC}}=-\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NA}}{\overline{NC}}\) mới đúng.

Sửa đề: AD=AC
a: Xét ΔACE và ΔADE có
AC=AD
\(\widehat{CAE}=\widehat{DAE}\)
AE chung
DO đó: ΔACE=ΔADE
Suy ra: \(\widehat{CAE}=\widehat{DAE}\)
hay AE là phân giác của góc CAB
b: Ta có: AC=AD
EC=ED
DO đó: AE là đường trung trực của CD
c: ta có: AE là đường trung trực của CD
nên AE\(\perp\)CD tại I
=>ΔAID vuông tại I
=>\(\widehat{ADI}< 90^0\)
=>\(\widehat{CDB}>90^0\)(Do góc ADI và góc CDB là hai góc kề bù)
Xét ΔCDB có \(\widehat{CDB}>90^0\)
nên BC là cạnh lớn nhất
=>BC>CD

Chắc là \(a\ne0\)
Pt hoành độ giao điểm: \(ax^2+bx+c=0\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}\\x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)
Do tọa độ đỉnh là (1;8) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\\dfrac{4ac-b^2}{4a}=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4ac-\left(-2a\right)^2=32a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+8\end{matrix}\right.\)
Mà \(MN=4\Leftrightarrow\left|x_1-x_2\right|=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=16\)
\(\Leftrightarrow\left(\dfrac{-2a}{a}\right)^2-4\dfrac{a+8}{a}=16\)
\(\Leftrightarrow a=-2\Rightarrow b=4\Rightarrow c=6\)

b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)

Giả sử M(m;0) và N(0;n)
\(\overrightarrow{AM}\left(m-4;-1\right)\)
\(\overrightarrow{NO}\left(0;-n\right)\)
\(\)Vì \(\overrightarrow{AM}=\overrightarrow{NO}\rightarrow\left\{{}\begin{matrix}m=4\\n=1\end{matrix}\right.\)
Khi đó ta tìm được pt (d): x+4y-4=0