Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Chỉ cần lấy M,N thuộc hai tia đối nhau Ox và Oy sao cho OM=ON(O là chân đường cao kẻ A xuống xy) thì ta được hai đường xiên AM=AN
b:
Trường hợp 1: D trùng với H thì AD=AH
=>AD>AM
Trường hợp 2: D nằm giữa M và H
=>HD<HM
=>AD<AM(hình chiếu, đường xiên)
Trường hợp 3: D nằm giữa H và N
=>HD<HN
=>AD<AN
mà AM=AN
nên AD<AM

a) Phân tích bài toán: Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN. Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM
Lời giải:
a) Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN.
Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM
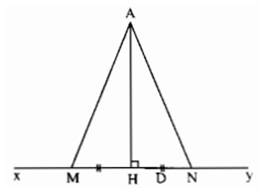


Gọi H là hình chiếu của A trên xy.
Để lấy hai điểm M, N thỏa mãn AM = AN ta vẽ 1 đường tròn tâm A, bán kính > AH cắt đường thẳng xy tại hai điểm M, N.