Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lỗi không vẽ được nha bạn !!!
a) Xét tứ giác ABOC có :
ABO + ACO = 90O + 90O =180O nên tứ giác ABOC nội tiếp ( đpcm )
b) Xét \(\Delta\)MBN và \(\Delta\)MCB có :
M chung
MBN = MCB ( cùng chắn cung BN )
=> \(\Delta\)MBN ~ \(\Delta\)MCB ( g - g ) nên \(\frac{MB}{MC}=\frac{MN}{MB}\Leftrightarrow MB^2=MN.MC\left(đpcm\right)\)
c) Xét \(\Delta\)MAN và \(\Delta\)MCA có góc M chung
Vì M là trung điểm của AB nên MA = MB
Theo câu b ta có : MA2 = MN . MC <=> \(\frac{MA}{MN}=\frac{MC}{MC}\)
Do đó \(\Delta\)MAN ~ \(\Delta\)MCA ( c - g - c )
=> góc MAN =góc MCA = góc NCA ( 1 )
mà : góc NCA = góc NDC ( cùng chắn cung NC ) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : góc MAN = góc NDC hay góc MAN = góc ADC (đpcm )

a.Vì MA,MB là tiếp tuyến của (O)
→ˆMAO=ˆMBO=90o→MAO^=MBO^=90o
→M,A,O,B→M,A,O,B thuộc đường tròn đường kình OM
b.Vì MA,MBMA,MB là tiếp tuyến của (O)→MO⊥AB=I→MO⊥AB=I
→OA2=OI.OM→OA2=OI.OM
C
Vì OF⊥CM=EOF⊥CM=E
→ˆFAC=ˆFEC=90o→◊AFCE,◊MAEO→FAC^=FEC^=90o→◊AFCE,◊MAEO nội tiếp
→M,A,E,O,B→M,A,E,O,B cùng thuộc một đường tròn
→ˆFCA=ˆFEA=ˆFBO→FCA^=FEA^=FBO^
→FC→FC là tiếp tuyến của (O)

Tự vẽ hình nhé!
a, MN;MP là 2 tiếp tuyến của đường tròn (O) (gt)
\(\Rightarrow\widehat{ONM}=\widehat{OPM}=90^0\Rightarrow\) Tứ giác MNOP nội tiếp ngược
\(\Rightarrow\widehat{NMO}=\widehat{NPO}\)( hai góc nội tiếp cùng chắn chung NO)
b, Gọi C là trung điểm dây AB ta có C cố định
(d) không qua O nên \(OC\perp AB\)
\(\widehat{OCM}=\widehat{OMN}=\widehat{OPM}=90^0\)
\(\Rightarrow\) C ; N ; P thuộc đường tròn đường kính OM
\(\Rightarrow\) C ; N ; P ; O ; M cùng thuộc một đường tròn
Mà O và C cố định
Do đó đường tròn ngoại tiếp tam giác MNP đi qua 2 điểm cố định O và C khi M lưu động trên đường thẳng (d)
c, Tứ giác MNOP là hình vuông
\(\Leftrightarrow\) Hình thoi MNOP có \(\widehat{ONM}=90^0\)
\(\Leftrightarrow\) Tứ giác MNOP có MN = ON = OP = PM và \(\widehat{ONM}=90^0\)
\(\Leftrightarrow\)Tam giác OMN vuông cân tại N \(\Leftrightarrow\) \(OM=ON\sqrt{2}=R\sqrt{2}\)
\(\Leftrightarrow\) M là giao điểm của đường tròn tâm O bán kính \(R\sqrt{2}\) và đường thẳng (d)
d, từ nghĩ đã...
\(\Leftrightarrow\) MN = ON = R ; \(\widehat{ONM}=90^0\)
cái dòng cuối cùng của ý d là dòng thứ 4 của ý c nhé, bị nhầm đó
d, Làm tiếp:
Giả sử đoạn thẳng OM cắt đường tròn (O) tại I'
OM là tia phân giác \(\widehat{NOP}\)( vì MN;MP là 2 tiếp tuyến của (O))
\(\Rightarrow\widehat{NOM}=\widehat{POM}\Rightarrow\widebat{NI'}=\widebat{PI'}\)
\(sđ\widehat{NPI'}=\frac{1}{2}sđ\widebat{NI'}\) ; \(sđ\widehat{MPI'}=\frac{1}{2}sđ\widehat{PI'}\)
Do đó \(\widehat{NPI'}=\widehat{MPI'}\Rightarrow\) PI' là tia phân giác \(\widehat{MPN}\)
\(\Delta MPN\)có MI' là tia phân giác \(\widehat{NMP}\)( vì MN và MP là 2 tiếp tuyến ) và PI' là tia phân giác \(\widehat{MPN}\)nên I' là tâm đường tròn nội tiếp tam giác MNP
Do đó \(I'\equiv I\)mà I' thuộc đường tròn (O;R)
Mặt khác : O , I cùng thuộc nửa mặt phẳng bờ d
Do đó I lưu động trên cung lớn AB của đưởng tròn tâm O bán kính R

C S N I M O K F A B D H
haizzz , vì mới lớp 8 nên mình chỉ làm được đến câu c, thôi , bạn thông cảm
a, Xét tam giác ABC vuông tại A và HA = HD
- Có \(\widehat{BAC}\)là góc nội tiếp đường tròn O chắn cung BC
- Mà BC là đường kính O
=> \(\widehat{BAC}=90^o\)
=> \(\Delta ABC\perp A\)
Xét \(\Delta OAD\)cân tại O ( Vì OA = OD do A , D cung thuộc O )
- Có AH là đường cao
=> OH là đường trung tuyến \(\Delta OAD\)
=> H là trug điểm AD
=> HA = HD
b, MN // SC , SC tiếp tuyến của (O)
Xét tam giác OSC có : M là trung điểm của OC
N là trung điểm của OS
=> MN là đường TB của \(\Delta OSC\)
=> MN // SC
Mà \(MN\perp OC\left(gt\right)\)
\(\Rightarrow OC\perp SC\)tại S
- Xét đường tròn O có CO là bán kính ( vì \(C\in\left(O\right)\)
\(CO\perp SC\)tại C
=> SC là tiếp tuyến của đường tròn (O)
c, BH . HC = AF . AK
Xét \(\Delta ABC\perp A\)có :
AH là đường cao
=> AH2 = BH . HC
Xét đường tròn đường kính AH có F thuộc đường tròn
\(\Rightarrow\widehat{AFH}=90^o\)
\(\Rightarrow HF\perp AK\)tại F
Xét tam giác AHK vuông tại H , ta có :
HF là đường cao
=> AH2 = AF . AK
=> BH . HC = AF . AK ( = AH2 )

A B C K M N H O
1) Dễ thấy ^CHN = ^CKN = 900 => Bốn điêm C,H,K,N cùng thuộc đường tròn đường kính CN
Hay tứ giác CNKH nội tiếp đường tròn (CN) (đpcm).
2) Sđ(BCnhỏ = 1200 => ^BOC = 1200 => ^BNC = 1/2.Sđ(BCnhỏ = 1/2.^BOC = 600
Vì tứ giác CNKH nội tiếp (cmt) nên ^KHC = 1800 - ^CNK = 1800 - ^BNC = 1200.
3) Hệ thức cần chứng minh tương đương với:
2KN.MN = AM2 - AN2 - MN2 <=> 2KN.MN = MN.MB - MN2 - AN2 (Vì AM2 = MN.MB)
<=> 2KN.MN = MN.BN - AN2 <=> AN2 = MN(BN - 2KN)
<=> AK2 + KN2 = MN(BK - KN) (ĐL Pytagoras) <=> AK2 + KN.KM = MN.BK
<=> AM2 - (MK2 - KN.KM) = MN.BK (ĐL Pytagoras) <=> AM2 - MK.MN = MN.BK
<=> AM2 = MN(BK + MK) = MN.MB <=> AM2 = AM2 (Hệ thức lượng đường tròn) (Luôn đúng)
Do đó hệ thức ban đầu đúng. Vậy KN.MN = 1/2.(AM2 - AN2 - MN2) (đpcm).

a) Xét tam giác DFB có:
\(\hept{\begin{cases}\widehat{D}=90^o\left(DE\perp AB\right)\\\widehat{C}=90^o\end{cases}}\)
=> Tứ giác DFBC nội tiếp
b) Xét tam giác BFG có \(\hept{\begin{cases}\widehat{FBG}=\frac{1}{2}\widebat{AG}\\\widehat{BGF}=\frac{1}{2}\widebat{AE}\end{cases}}\)
Mà cung AB= cùng BG
=> BF=BG

\(\text{a) Xét tứ giác ADMO có:}\)
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> ∠DMO + ∠DAO = 180o
=> Tứ giác ADMO là tứ giác nội tiếp.
\(\text{b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM}\)
=>(AOD = \(\frac{1}{2}\)∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
=> ∠ABM = \(\frac{1}{2}\)∠AOM
=> ∠AOD = ∠ABM
Mà 2 góc này ở vị trí đồng vị
=> OD // BM
Xét tam giác ABN có:
OM// BM; O là trung điểm của AB
=> D là trung điểm của AN
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
=>OB ⊥ BE
Vậy BE là tiếp tuyến của (O).
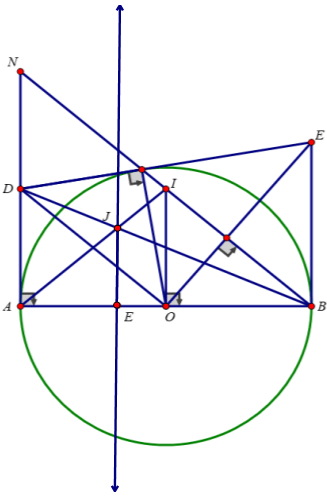
d) Lấy điểm E trên tia OA sao cho OE = \(\frac{OA}{3}\)
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
Ta có:
\(\hept{\begin{cases}\widehat{IBA}=\widehat{IAB}\\\widehat{IBA}+\widehat{INA}=90^0\\\widehat{NAI}+\widehat{IAB}=\widehat{NAB}=90^0\end{cases}}\)
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
Xét ΔBNA có:
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
Xét tam giác AIO có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}=\frac{2}{3}\Rightarrow\text{JE}\text{//}OI\)
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J' bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}\)
\(\text{MÀ}\frac{AE}{AO}=\frac{2}{3}\Rightarrow\frac{\text{AJ}}{AI}=\frac{2}{3}\)
AI là trung tuyến của tam giác NAB
=> J' là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
HÌNH Ở TRONG THỐNG KÊ HỎI ĐÁP NHA

Mình chỉ biết làm câu a, thoi nhé thông cảm , :<<<<
a, Ta có : \(OB \perp AB\Rightarrow\widehat{oBa}=90^o\)
\(OC \perp AC \Rightarrow\widehat{oCa}=90^o\)
Xét tứ giác ABOC có : \(\widehat{oBa}=\widehat{oCa}=90^o\)
=> Tứ giác ABOC nội tiếp ( Tổng 2 góc = 180o )