Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔMNP có
NQ là đường cao ứng với cạnh MP
PR là đường cao ứng với cạnh MN
MP cắt MN tại S
Do đó: MS\(\perp\)NP
b) Ta có: MS\(\perp NP\)(cmt)
nên \(\widehat{SMN}+\widehat{MNP}=90^0\)
hay \(\widehat{SMN}=25^0\)

Vì \(\Delta ABC=\Delta MNP\) nên:
N = B = 60o (2 góc tương ứng)
C = P = 30o (2 góc tương ứng)
Nên A = M = 180o - (60o + 30o) = 90o
Vậy \(\Delta ABC,\Delta MNP\) là các tam giác vuông (có góc bằng 90o)

Câu 1:
Giải:
Ta có: \(15x=\left(-10\right)y=6z\Rightarrow\frac{15x}{30}=\frac{\left(-10\right)y}{30}=\frac{6z}{30}\Rightarrow\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}\)
Đặt \(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=k\)
\(\Rightarrow x=2k,y=-3k,z=5k\)
Mà \(xyz=-30000\)
\(\Rightarrow2k\left(-3\right)k5k=-30000\)
\(\Rightarrow\left(-30\right).k^3=-30000\)
\(\Rightarrow k^3=1000\)
\(\Rightarrow k=10\)
\(\Rightarrow x=20;y=-30;z=50\)
Vậy bộ số \(\left(x;y;z\right)\) là \(\left(20;-30;50\right)\)
Câu 3:
Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3b}=\frac{b}{3c}=\frac{c}{3d}=\frac{d}{3a}=\frac{a+b+c+d}{3b+3c+3d+3a}=\frac{a+b+c+d}{3\left(a+b+c+d\right)}=\frac{1}{3}\)
\(\frac{a}{3b}=\frac{1}{3}\Rightarrow3a=3b\Rightarrow a=b\)
Tương tự ta có b = c, c = d, d = a
\(\Rightarrow a=b=c=d\)
\(\Rightarrowđpcm\)
3, áp dụng tính chất dãy tỉ số bằng nhau:
=>\(\frac{a}{3.b}\)=\(\frac{b}{3.c}\)=\(\frac{c}{3.d}\) =\(\frac{d}{3.a}\) =\(\frac{a+b+c+d}{3\left(b+c+a+d\right)}\) =\(\frac{1}{3}\)
\(\Rightarrow\)\(\frac{a}{3b}\)=\(\frac{1}{3}\) =>\(\frac{1.b}{3.b}\) =\(\frac{b}{3.b}\) =>\(\frac{a}{3b}\) =\(\frac{b}{3b}\) =>...a=b (1)
\(\frac{c}{3d}\)=\(\frac{1}{3}\) =>\(\frac{1.d}{3.d}\) =\(\frac{d}{3d}\) =>\(\frac{c}{3d}\) =\(\frac{d}{3d}\) =>...c=d (2)
\(\frac{b}{3c}\) =\(\frac{1}{3}\) =>\(\frac{1.c}{3.c}\) =\(\frac{c}{3c}\)=>\(\frac{b}{3c}\) =\(\frac{c}{3c}\)=>..b=c (3)
\(\frac{d}{3a}\)=\(\frac{1}{3}\) =>\(\frac{1.a}{3.a}\) =\(\frac{a}{3a}\)=>\(\frac{d}{3a}\) =\(\frac{a}{3a}\)...=>d=a (4)
từ (1).(2).(3)(4)=>a=b=c=d(dpcm)
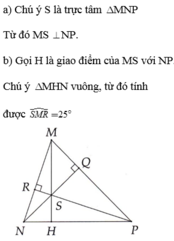
a) Theo đề ta có S là trực tâm của tam giác MNP và MNP là tam giác nhọn
Suy ra MS cũng là đường cao đáy NP, hay \(MS\perp NP\)
b) Gọi O là giao điểm của MS và NP. Ta có MNO là tam giác vuông tại O
Suy ra \(\widehat{MNO}+\widehat{NMO}=90^o\) hay \(\widehat{MNP}+\widehat{SMR}=90^o\)
Suy ra \(\widehat{SMR}=90^o-\widehat{MNP}=90^o-65^o=25^o\)