Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D N E M I K 1 2 1 1
Giải: Xét t/giác ABE và t/giác ANM
có: AB = BN (gt)
\(\widehat{B_1}=\widehat{N_1}\) (slt của AE // MN)
\(\widehat{B_1}=\widehat{B_2}\) (đối đỉnh)
=> t/giác ABE = t/giác ANM (g.c.g)
=> EA = AM (2 cạnh t/ứng)
Xét tứ giác EBMN có AB = AN (gt)
EA = MA (cmt)
=> tứ giác EBMN là hình bình hành
có BN \(\perp\)EM (gt)
=> EBMN là hình thoi
Để hình thoi EBMN là hình vuông
<=> EM = BN <=> AB = AM
do AM = MC = 1/2AC
<=> AB = 1/2AC
<=> AC = 2AB
Vậy để tứ giác EBMN là hình vuông <=> t/giác ABC có AC = 2AB

MK dang thac mac tai sao mk lai co the lam ging het bn 100% ?


Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

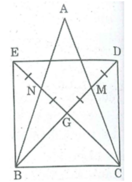
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ∆ ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN, có: BC cạnh chung
∠ (BCM) = ∠ (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ∆ BCM = ∆ CBN (c.g.c)
⇒ ∠ (MBC) = ∠ (NCB) ⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.

Tự vẽ hình:
cminh:Vì D đối xứng với G qua M
=>GM=MD Hay GD=2GM
Vì BM;CN cắt nhau tại G trong tam giác ABC
=>G là trọng tâm trong Tam giác ABC =>BG=2GM
Suy ra : GD=BG(vì =2GM)=> G là trung điểm của BD (1)
Ta lại có : E đối xứng với G qua N=> EN=GN Hay EG=2NG
Và CG=2GN( G là trọng tâm)
Suy ra: CG=EG ( vì =2NG) (2) (*)
Từ (1) (2)=> Tứ giác BEDC là hình bình hành
Xét \(\Delta\)CBM Và \(\Delta\)BCN Có:
BC: Cạnh chung
Góc B=C(g/t)
BN=CM(AB=AC)
=> hai tam giác bằng nhau(c-g-c)
=>MBC=NCB(2 góc tương ứng) hay tam giác GBC cân=> BG=GC (**)
Từ (*) (**)=> Hình bình hành BEDC là hình chữ nhật
a, Xét tam giác ABC có BN=NA(gt) , CM=MA(gt)
=> NM là đg tb =>NM // BC và NM=1/2 BC
=> Tứ giác BNMC là hthang
lại có \(\widehat{ABC}=\widebat{ACB\left(gt\right)}\)
=> Tứ giác BNMC là hthang cân