Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có tứ giác MHNA là hình chữ nhật
\(\Rightarrow\widehat{AMN}=\widehat{AHN}\) ( góc nội tiếp cùng chắn cung AN)
mà \(\widehat{AHN}=\widehat{ACH}\) ( cùng phụ với \(\widehat{HAN}\) )
\(\Rightarrow\widehat{AMN}=\widehat{ACH}\)
Xét \(\Delta AMN\) và \(\Delta ACB\) có:
\(\left\{{}\begin{matrix}\widehat{AMN}=\widehat{ACH}\left(cmt\right)\\\widehat{MAN}chung\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(g.g\right)\)
\(\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\Rightarrow AM.AB=AN.AC\left(đpcm\right)\)
b) Xét \(\Delta AHB\) vuông tại H, \(MH\perp AB\) có:
\(MH^2=MA.MB\left(1\right)\)
cmtt: \(NH^2=NA.NC\left(2\right)\)
Ta lại có: \(HB.HC=AH^2=MN^2\)( 2 đường chéo bằng nhau) (3)
Xét \(\Delta MHN\) vuông tại H có
\(\Rightarrow MH^2+HN^2=MN^2=AH^2\left(4\right)\)
Từ (1),(2),(3) và (4) \(\Rightarrow HB.HC=MA.MB+NA.NC\left(đpcm\right)\)
c) Có \(HB=\frac{AC^2}{BC}\)
\(HC=\frac{AC^2}{BC}\)
\(\Rightarrow\frac{BH}{HC}=\frac{AB^2}{BC}:\frac{AC^2}{BC}=\frac{AB^2}{AC^2}=\left(\frac{AB}{AC}\right)^2\)

A B C H N M 3 4
Xét \(\Delta HAC\)vuông tại H có HN là đường trung tuyến ứng với cạnh huyền
=> HN = NC = NA = AC/2
=> AC = 2HN = 8
Tương tự AB = 6
Theo hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A có AH là đường cao thì
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)
\(\Leftrightarrow AH=\frac{24}{5}\)
Áp dụng định lí Pytago vào \(\Delta HAC\)vuông tại H có
\(HA^2+HC^2=AC^2\)
\(\Leftrightarrow\left(\frac{24}{5}\right)^2+HC^2=8^2\)
\(\Leftrightarrow HC=\frac{32}{5}\)
Tương tự \(HB=\frac{18}{5}\)

A B C H M N
Vì M là trung điểm của AB => HM là trung tuyến
Mà \(\Delta ABH\)vuông tại H
=> \(HM=\frac{1}{2}AB\)( trong tam giác vuông trung tuyến ứng với cạnh huyền = 1 phần 2 cạnh huyền )
=> AB = 30 cm
Chứng minh tương tự
=> AC= 40 cm
Xét \(\Delta ABC\)có ( A = 900 )
=> \(BC=\sqrt{AC^2+AB^2}=50\)cm
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Rightarrow\frac{1}{AH}=\sqrt{\frac{1}{AB^2}+\frac{1}{AC^2}}=\frac{1}{24}\)
\(\Rightarrow AH=24cm\)
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(AB^2=BH.BC\)
\(\Rightarrow BH=AB^2:BC=18cm\)
Vì BH + HC = BC
\(\Rightarrow HC=50-18=32cm\)
Study well

a/ Có tứ giác MHNA là hcn\(\Rightarrow\widehat{AMN}=\widehat{AHN}\) (góc nt cùng chắn \(\stackrel\frown{AN}\))
Mà \(\widehat{AHN}=\widehat{ACH}\) (cùng phụ vs \(\widehat{HAN}\))
\(\Rightarrow\widehat{AMN}=\widehat{ACH}\)
Xét \(\Delta AMN\) và \(\Delta ACB\) có:
\(\widehat{AMN}=\widehat{ACH}\left(CMT\right)\)
\(\widehat{MAN}\) : góc chung
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(gg\right)\)
\(\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\Leftrightarrow AM.AB=AN.AC\)
b/ Có \(HB=\frac{AB^2}{BC}\)
\(HC=\frac{AC^2}{BC}\)
\(\Rightarrow\frac{HB}{HC}=\frac{\frac{AB^2}{BC}}{\frac{AC^2}{BC}}=\frac{AB^2}{AC^2}=\left(\frac{AB}{AC}\right)^2\)
c/ Xét \(\Delta AHB\) vuông tại H,\(MH\perp AB\)
\(\Rightarrow MA.MB=MH^2\)(1)
tương tự\(\Rightarrow NA.NC=HN^2\) (2)
\(HB.HC=AH^2=MN^2\) (2 đường chéo bằng nhau)(3)
Xét \(\Delta MHN\) vuông tại H
\(\Rightarrow MH^2+HN^2=MN^2=AH^2\)(4)
Từ (1),(2),(3),(4)\(\Rightarrow HB.HC=MA.MB+NA.NC\)

a) Áp dụng hệ thức lượng trong \(\Delta vAHB\), ta có:
\(AH^2=AM\cdot AB\left(1\right)\)
Áp dụng hệ thức lượng trong \(\Delta vAHC\), ta có:
\(AH^2=AN\cdot AC\left(2\right)\)
Từ(1) và (2) ta được: \(AM\cdot AB=AN\cdot AC\)
b) Ta có: MHNA là hình chữ nhật(pn tự cm nha cái này dễ)
\(\Rightarrow MH=AN\)
Áp dụng hệ thức lượng trong \(\Delta vAHC\), ta có:
\(HN^2=AN\cdot NC\)
Áp dụng hệ thức lượng trong \(\Delta vAHB\), ta có:
\(HM^2=AM\cdot MB\)
Áp dụng hệ thức lượng trong \(\Delta vAHN\), ta có:
\(AN^2+HN^2=AH^2\)
Mà \(MH=AN\)
\(\Rightarrow MH^2+HN^2=AH^2\)
\(\Rightarrow BM\cdot MA+AN\cdot NC=BH\cdot HC\)
c) Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AC^2=HC\cdot BC\left(1\right)\)
Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AB^2=HB\cdot BC\left(2\right)\)
Lấy (2) chia (1) ta được: \(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
d) Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AC^2=HC\cdot BC\Rightarrow AC^4=HC^2\cdot BC^2\)
\(\Rightarrow AC^4=NC\cdot AC\cdot BC^2\Rightarrow AC^3=NC\cdot BC^2\left(1\right)\)
Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AB^2=HB\cdot BC\Rightarrow AB^4=HB^2\cdot BC^2\)
\(\Rightarrow AB^4=BM\cdot AB\cdot BC^2\Rightarrow AB^3=BM\cdot BC^2\left(2\right)\)
Lấy (2) chia (1) ta được: \(\dfrac{BM}{CN}=\left(\dfrac{AB}{AC}\right)^3\)

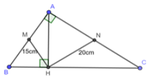
Xét ∆ ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = 1 2 AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ∆ ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = 1 2 AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
![]()
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D
B M A N C H
Tam giác AHB vuông tại H có HM là trung tuyến
=> HM = 1/2 AB => AB = 30 cm
Tam giác AHC vuông tại H có HN là trung tuyến
=> HN = 1/2 AC => AC = 40 cm
Áp dụng Pytago ta có: AB2 + AC2 = BC2
=> BC2 = 302 + 402 = 2500
=> BC = 50
Áp dụng hệ thức lượng ta có:
AB2 = BH.BC => \(BH=\frac{AB^2}{BC}=18\)
AC2 = CH.BC => \(CH=\frac{AC^2}{BC}=32\)
HA.BC = AB.AC => \(HA=\frac{AB.AC}{BC}=24\)