Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

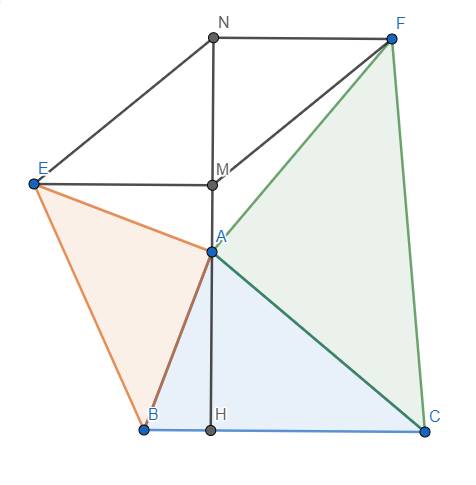
a) Do tam giác AEB vuông cân tại A nên \(\left\{{}\begin{matrix}\widehat{EAB}=90^o\\AE=AB\end{matrix}\right.\)
Ta thấy \(\widehat{MEA}=\widehat{BAH}\) vì chúng cùng phụ với \(\widehat{EAM}\)
Xét 2 tam giác HAB vuông tại H và MEA vuông tại M, ta có:
\(AE=AB\left(cmt\right),\widehat{MEA}=\widehat{BAH}\left(cmt\right)\)
\(\Rightarrow\Delta HAB=\Delta MEA\left(ch-gn\right)\) \(\Rightarrow AH=ME\) (1)
Tương tự, ta cũng có \(\Delta HAC=\Delta NFA\Rightarrow HC=AN\) (2)
Từ (1) và (2) suy ra \(EM+HC=AH+AN\) hay \(EM+HC=HN\) (đpcm)
b) Từ \(\Delta HAC=\Delta NFA\Rightarrow AH=NF\)
Từ đó suy ra \(ME=NF\left(=AH\right)\)
Xét tam giác MNE và NMF, ta có:
\(ME=NF\left(cmt\right),\widehat{EMN}=\widehat{FNM}\left(=90^o\right)\), MN là cạnh chung.
\(\Rightarrow\Delta MNE=\Delta NMF\left(c.g.c\right)\)
\(\Rightarrow\widehat{ENM}=\widehat{FMN}\) \(\Rightarrow\) EN//FM (2 góc so le trong bằng nhau)
Ta có đpcm.

a) Xét ∆AHB,∆EMA có :
^AHB = ^EMA = 90o
AB = AE (gt)
Do đó : ∆AHB = ∆EMA (ch-gn)
b) ∆AHB = ∆EMA (ch-gn)
=> EM = AH (1)
Cmtt ta cũng có : ∆AHC = ∆FNA (Ch-Gn)
=> HC = NA (2)
Từ (1)(2) => EM + HC = AH + NA
=> EM + HC = NH (A nằm giữa H,N)
d) Có : EM _|_ AH
FN _|_ AH
=> EM // FN

a.a. Ta có :
ΔAHB=ΔEMA(ch−gn)ΔAHB=ΔEMA(ch−gn)
AHBˆ=EMAˆ=(900)AHB^=EMA^=(900)
AB=AE(gt)AB=AE(gt)
ΔBAH=ΔAEMΔBAH=ΔAEM ( cùng phụ với ΔMAEΔMAE )
⇒EM=AH(1)⇒EM=AH(1)EM = AH (1)
Tương tự:
ΔAHC=ΔFNA(ch−gn)ΔAHC=ΔFNA(ch−gn)
⇒HC=NA(2)⇒HC=NA(2)
Từ (1)(1) và (2)(2) ⇒EM+HC=AH+NA=NH⇒EM+HC=AH+NA=NH
b) Từ ΔAHC=ΔFNAΔAHC=ΔFNA
⇒AH=NF(3)⇒AH=NF(3)
Từ (1)(1) và (3)(3)EM=MFEM=MF
Mặt khác : EM // NF ( cùng vuông góc với AH )
Ta suy ra : EN // FM

a) xét tg EAC và tg BAF
có: EA = BA (gt); ^EAC =^BAF ( ^EAB = ^ FAC = 90 độ, ^BAC chung); AC = AF(gt)
=> tg EAC = tg BAF(c-g-c)
=> EC = BF ( 2 cạnh t/ư)
b) Kẻ \(EG\perp AH⋮G;FK\perp AH⋮K\)
xét tg EGA vuông tại G và tg AHB vuông tại H
có: EA = AB (gt); ^EAG =^ABH ( cùng phụ với ^BAH)
=> tg EGA = tg AHB( ch-gn)
=> EG = AH ( 2 cạnh t/ư) (1)
chứng minh tương tự, có: tg AFK = tg CAH(ch-gn)
=> FK = AH (2 cạnh t/ư) (2)
Từ(1);(2) => EG = FK (=AH)
xét tg EGI vuông tại G và tg FKI vuông tại K
có: EG = FK (cmt); ^EIG = ^FIK (đ đ)
=> tg EGI = tg FKI ( cgv -gn)
=> EI = FI (2 canh t/ư)
=> I là trung điểm của EF
...
hình bn tự kẻ nha
B C A E F H M N
Xét ∆AHB,∆EMA có :
^AHB = ^EMA = 90o
AB = AE (gt)
^BAH = ^AEM (vì cùng phụ với ^MAE)
Do đó : ∆AHB = ∆EMA (Ch - Gn)
=> EM = AH (1)
Cmtt ta cũng có : ∆AHC = ∆FNA (Ch-Gn)
=> HC = NA (2)
Từ (1)(2) => EM + HC = AH + NA
=> EM + HC = NH (A nằm giữa H,N)
b) Có : EM _|_ AH
FN _|_ AH
=> EM // FN