Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Xét hai tg vuông BKC và tg vuông CHB có
Cạnh huyền BC chung (1)
\(S_{ABC}=\frac{AB.CK}{2}=\frac{AC.BH}{2}\) Mà AB=AC => BH=CK (2)
Từ (2) Và (2) => tg BKC = tg CHB (cạnh huyền và cạnh góc vuông tương ứng bằng nhau) => BK=CH (*)
Mà AB=AC=AK+BK=AH+CH => AK=AH => tg AKH cân tại A
+ Xét tg cân AKH có
^AKH=^AHK=(180-^BAC)/2 (3)
+ Xét tg cân ABC có
^ABC=^ACB=(180-^BAC)/2 (4)
Từ (3) và (4) => ^AKH=^ABC => KH//BC (có hai góc đồng vị bằng nhau) (**)
Từ (*) và (**) => BKHC là hình thang cân

a)Tam giác KBC=tam giácHCB(cạnh huyền góc nhọn)
=>BH=CK ; BK=CH
Mà AB=AC=>AK=KH=>Tam giác AKH cân tại A
=>Góc AKH=Góc KBC mà 2 góc đồng vị
=>KH//BC=>KHCB là hình thang,có BH=CK
=>KHCB là hình thang cân
b)Tứ giác KIBM có:KH=BM ; KH//BM
=>KHBM là hình bình hành
=>KB=HM
Mà HC=KB
=>HC=MH=> Tam giác HMC cân tại H
c)Để A,O,M thẳng hàng thì tam giác ABC phải là tam giác đều (bạn tự chứng minh nha)
Chúc bạn học tốt!!

vì tứ giác FMEH có góc F = 90 độ; H = 90 độ; E = 90 độ.
\(\Rightarrow\)góc M = 90 độ
\(\Rightarrow FH//ME ; FM//HE\)
\(\Rightarrow\)tứ giác FMEH là hình chữ nhật
\(\Rightarrow\)ME=FH
a ) tứ giác MFHE có :
\(\widehat{MFH}+\widehat{FHE}+\widehat{HEM}+\widehat{EMF}=360^o\)( tính chất tổng các góc trong tứ giác )
hay \(90^o+90^o+90^o+\widehat{EMF}=360^o\)
\(\Rightarrow\widehat{EMF}=360^o-90^o-90^o-90^o\)
\(\Rightarrow\widehat{EMF}=90^o\)
\(\Rightarrow FM\perp ME\left(dhnb\right)\)
mà \(HE\perp ME\left(gt\right)\)
\(\Rightarrow FM//HE\left(\perp\rightarrow//\right)\)
\(\Rightarrow FHEM\)là hình thang
mà\(\widehat{MFH}=\widehat{EMF}\left(=90^o\right)\)
\(\Rightarrow FHEM\)là hình thang cân
\(\Rightarrow ME=FH\)( tính chất cạnh trong hình thang cân )
b ) kẻ EF
có M là trung điểm của BC ( gt )
\(\Delta ABC\)cân tại A ( gt )
\(\Rightarrow AM\)là đường cao
\(\Rightarrow AM\)cũng là tia phân giác của \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAM}=\widehat{CAE}\)\(hay\widehat{DAM}=\widehat{EAM}\)
xét \(\Delta MAD\)và \(\Delta MCE\)có
\(\hept{\begin{cases}\widehat{ADM}=\widehat{AEM}=90^o\\AMchung\\\widehat{DAM}=\widehat{EAM}\left(cmt\right)\end{cases}}\)
\(\Rightarrow\Delta MAD=\Delta MCE\left(ch-gn\right)\)
\(\Rightarrow AD=AE\)( 2 cạnh tương ứng )
xét \(\Delta ADK\)và \(\Delta AEK\)có :
\(\hept{\begin{cases}AMchung\\\widehat{DAK}=\widehat{EAK}\left(cmt\right)\\AD=AE\left(cmt\right)\end{cases}}\)
\(\Rightarrow\Delta ADK=\Delta AEK\left(c-g-c\right)\)
\(\Rightarrow\widehat{AKD}=\widehat{AKE}\)( 2 góc tương ứng )
mà \(\widehat{AKD}+\widehat{AKE}=180^o\left(kb\right)\)
\(\Rightarrow\widehat{AKD}=\widehat{AKE}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AM\perp DK\left(dhnb\right)\)
AM là đường cao \(\Rightarrow AM\perp BC\)
\(\Rightarrow DK//BC\)
\(hayBK//MC\)
\(\Rightarrow MDKC\)là hình thang

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
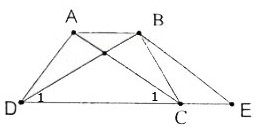
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 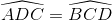
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:

AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 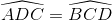
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Ta có ΔABH=ΔACK ( cạnh huyền- góc nhọn)
⇒ AH=AK
⇒ ΔAHK cân tại A
Nên ∠AKH=∠AHK =\(\dfrac{180^0-A}{2}\)
Mà ΔABC cân tại A (gt)
⇒ ∠ABC=∠ACB= \(\dfrac{180^0-A}{2}\)
Nên ∠AKH=∠ABC
Mà hai góc này ở vị trí đồng vị
⇒ HK//BC
Nên BKHC là hình thang
Có ∠ABC=∠ACB (gt)
Vậy BKHC là hình thang cân