Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u_1=\sqrt{3}=tan\frac{\pi}{3}\)
Mặt khác \(tan\frac{\pi}{8}=\sqrt{2}-1\Rightarrow u_{n+1}=\frac{u_n+tan\frac{\pi}{8}}{1-u_n.tan\frac{\pi}{8}}\)
Nhìn công thức \(u_{n+1}\) có dạng \(tan\left(a+b\right)\) nên ta thay thử vài giá trị tìm quy luật
\(u_2=\frac{u_1+tan\frac{\pi}{8}}{1-tan\frac{\pi}{8}.u_1}=\frac{tan\frac{\pi}{3}+tan\frac{\pi}{8}}{1-tan\frac{\pi}{8}.tan\frac{\pi}{3}}=tan\left(\frac{\pi}{3}+\frac{\pi}{8}\right)\)
\(u_3=\frac{tan\left(\frac{\pi}{3}+\frac{\pi}{8}\right)+tan\frac{\pi}{8}}{1-tan\left(\frac{\pi}{3}+\frac{\pi}{8}\right).tan\frac{\pi}{8}}=tan\left(\frac{\pi}{3}+\frac{\pi}{8}+\frac{\pi}{8}\right)=tan\left(\frac{\pi}{3}+2.\frac{\pi}{8}\right)\)
Dự đoán số hạng tổng quát có dạng: \(u_n=tan\left(\frac{\pi}{3}+\left(n-1\right)\frac{\pi}{8}\right)\)
Giả sử công thức đúng với \(n=k\) hay \(u_k=tan\left(\frac{\pi}{3}+\left(k-1\right)\frac{\pi}{8}\right)\)
Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay \(u_{k+1}=tan\left(\frac{\pi}{3}+k\frac{\pi}{8}\right)\)(các số hạng đầu đã kiểm tra nên chứng minh quy nạp chắc khỏi cần kiểm tra lại)
Thật vậy, với \(n=k+1\) ta có:
\(u_{k+1}=\frac{u_k+tan\frac{\pi}{8}}{1-u_k.tan\frac{\pi}{8}}=\frac{tan\left(\frac{\pi}{3}+\left(k-1\right)\frac{\pi}{8}\right)+tan\frac{\pi}{8}}{1-tan\frac{\pi}{8}.tan\left(\frac{\pi}{3}+\left(k-1\right)\frac{\pi}{8}\right)}\)
\(=tan\left(\frac{\pi}{3}+\left(k-1\right)\frac{\pi}{8}+\frac{\pi}{8}\right)=tan\left(\frac{\pi}{3}+k\frac{\pi}{8}\right)\) (đpcm)

S= u1.u1 + u2.u2+...+un.un
S = u1.(u2 - d) + u2.(u3 - d)+...+un(un+1 - d)
S = u1.u2 + u2.u3 +...+un.un+1-d(u1+u2+...+un)
Đặt A = u2.u3 + u3.u4+...+un.un+1
3d.A = u2.u3.(u4-u1) + u3.u4.(u5-u2)+...+un.un+1.(un+2-un-1)
3d.A = u2.u3.u4 - u1.u2.u3 + u3.u4.u5 - u2.u3.u4+...+un.un+1.un+2 - un-1.un.un+1
3d.A = un.un+1.un+2 - u1.u2.u3
3d.A = (u1 + d.n - d)(u1 + d.n)(u1 + d.n + d) - u1.(u1+d).(u1+2.d)
A = [(u1 + d.n - d)(u1 + d.n)(u1 + d.n + d) - u1.(u1+d).(u1+2.d)]/(3.d)
S = A + u1.(u1 + d) + d[2.u1+(n-1).d].n/2

Ý bạn là dãy số này: \(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+\left(\dfrac{1}{2}\right)^n\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1=1\\u_{n+1}+2.\left(\dfrac{1}{2}\right)^{n+1}=u_n+2.\left(\dfrac{1}{2}\right)^n\end{matrix}\right.\)
Đặt \(v_n=u_n+2.\left(\dfrac{1}{2}\right)^n\Rightarrow\left\{{}\begin{matrix}v_1=u_1+2\left(\dfrac{1}{2}\right)=2\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow v_n=v_1=1\Rightarrow u_n+2\left(\dfrac{1}{2}\right)^n=1\)
\(\Rightarrow u_n=1-2\left(\dfrac{1}{2}\right)^n\)
\(\Rightarrow lim\left(u_n\right)=lim\left[1-2\left(\dfrac{1}{2}\right)^n\right]=1-0=1\)
Chọn B.
Ta có: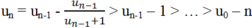
Suy ra: un+1 > u0 – (n – 1) = 2012 – n
Mặt khác: un = (un – un-1) + (un-1 – un-2) + … + (u1 – u0) + u0
Mà:
Suy ra un < u0 – n + 1 = 2012 – n
Do đó: 2011 – n < un < 2012 – n ⇒ [un] = 2011 – n
Vì u0 = 2011 và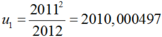
nên [u0] = 2011 – 0, [u1] = 2010 = 2011 – 1
Vậy [un] = 2011 – n,