
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Năm số hạng đầu là 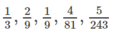
b) Lập tỉ số
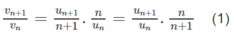
Theo công thứcđịnh nghĩa ta có 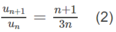
Từ (1) và (2) suy ra

Vậy, dãy số ( v n ) là cấp số nhân, có v 1 = 1 / 3 , q = 1 / 3
c) Để tính ( u n ) , ta viết tích của n - 1 tỉ số bằng 1/3
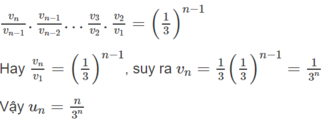

Chọn A.
Ta có: 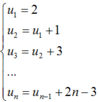
Cộng hai vế ta được un = 2 + 1 + 3 + 5 + … + (2n – 3) = 2 + (n – 1)2

a. 5 số hạng đầu dãy là:
u1 = 2;
u2 = 2u1 – 1 = 3;
u3 = 2u2 – 1 = 5;
u4 = 2u3 – 1 = 9;
u5 = 2u4 – 1 = 17
b. Chứng minh un = 2n – 1 + 1 (1)
+ Với n = 1 ⇒ u1 = 21 - 1 + 1 = 2 (đúng).
+ Giả sử (1) đúng với n = k ≥ 1, tức là uk = 2k-1 + 1 (1)
Ta chứng minh: uk+1 = 2k + 1. Thật vậy, ta có:
⇒ uk+1 = 2.uk – 1 = 2(2k-1 + 1) – 1 = 2.2k – 1 + 2 – 1 = 2k + 1
⇒ (1) cũng đúng với n = k + 1 .
Vậy un = 2n – 1 + 1 với mọi n ∈ N.

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.

Chọn B.
Phương pháp:
Công thức tính tổng n số hạng đầu tiên của cấp số cộng có số hạng đầu u1 và công sai d
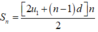
Cách giải:
Ta có: u n + 1 = u n + 2 , ∀ n ∈ ℕ *
⇒ ( u n ) là cấp số cộng có u 1 = - 5 , d = 2
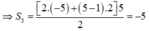
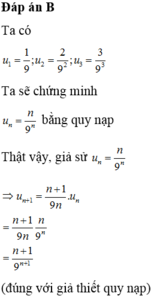




Tham khảo:
Câu 5 ạ - Hoc24