Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


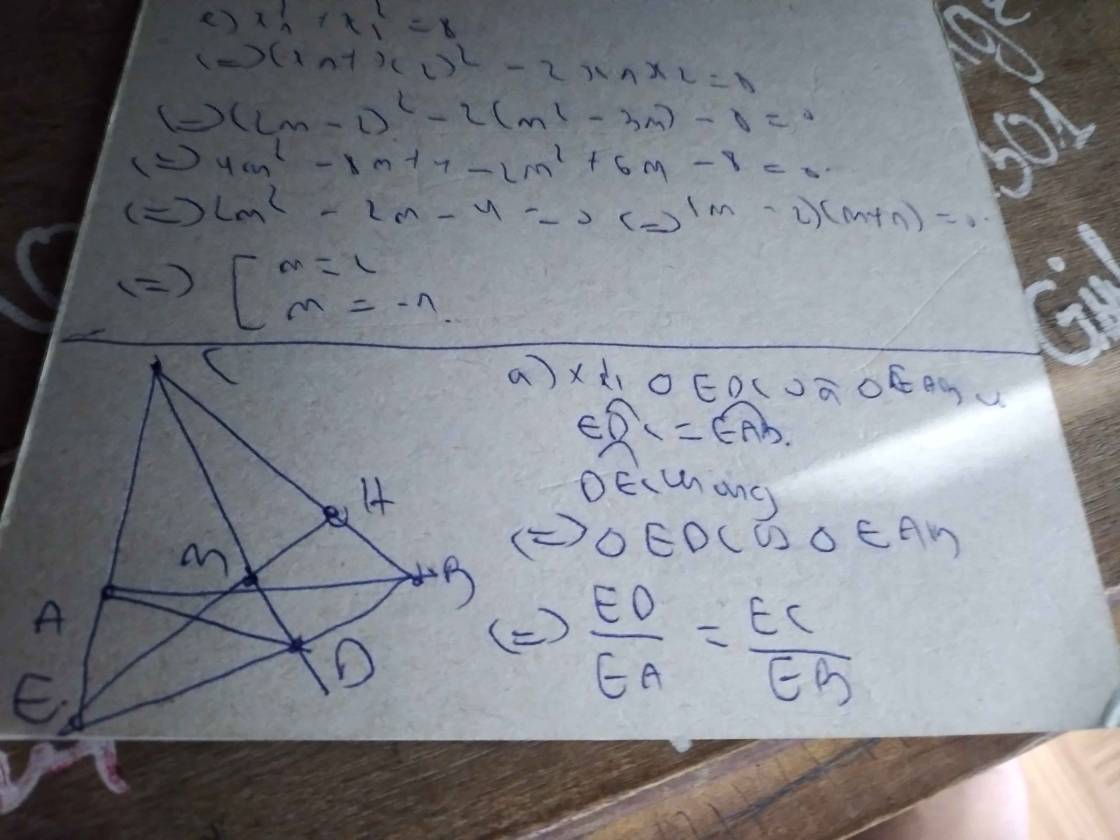
E A C H B D
bài giảng ở đây nha
Câu hỏi của Quỳnh Hoa Lenka - Toán lớp 8 | Học trực tuyến
vào thống kê hỏi đáp của mình có chữ màu xanh ở câu trả lời này nhấn zô đó sẽ ra
hc tốt ~:B~

Câu 3 : Chỉ là kẻ BD, CM ko thôi sao? thế thì M và D nằm đâu trên 2 cạnh AB và AC cũng đc? Như thế sẽ ko làm được bạn nhé
Câu 5 :
\(2\left(y^2+yz+z^2\right)+3x^2=36\)
\(\Leftrightarrow2y^2+2yz+2z^2+3x^2=36\)
\(\Leftrightarrow2y^2+2yz+2z^2+3x^2+2xy+2zx=36+2xy+2zx\)
\(\Leftrightarrow\left(x^2+y^2+z^2+2xy+2yz+2zx\right)+\left(x^2-2xy+y^2\right)+\left(x^2-2zx+z^2\right)=36\)
\(\Leftrightarrow\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2=36\)
\(\Leftrightarrow\left(x+y+z\right)^2=36-\left(x-y\right)^2-\left(x-z\right)^2\le36\)
\(\Leftrightarrow-6\le x+y+z\le6\)
_Minh ngụy_

A B C D M E H
a)
Tam giác AEB vuông tại A và tam giác DEC vuông tại D có:
AEB = DEC
=> Tam giác AEB ~ Tam giác DEC (g - g)
=> \(\dfrac{AE}{DE}=\dfrac{EB}{EC}\)
=> EB . DE = AE . EC
b)
Tam giác EBC có: CD là đường cao và BA là đường cao
CD cắt BA tại M
=> M là trực tâm của tam giác EBC
=> EM _I_ tại H (H thuộc BC)
Tam giác HBE vuông tại H và tam giác DBC vuông tại D có:
HBE = DBC
=> Tam giác HBE ~ Tam giác DBC (g - g)
=> \(\dfrac{HB}{DB}=\dfrac{BE}{BC}\)
=> DB . BE = HB . BC
Tam giác HCE vuông tại H và tam giác ACB vuông tại A có:
HCE = ACB
=> Tam giác HCE ~ Tam giác ACB (g - g)
=> \(\dfrac{HC}{AC}=\dfrac{CE}{CB}\)
=> HC . CB = AC . CE
Ta có : DB . BE + AC . CE = HB . BC + HC . CB = BC . (HC + HB) = BC . BC = BC2
c)
Tam giác EDA và tam giác ECB có:
DEA = CEB
\(\dfrac{DE}{CE}=\dfrac{EA}{EB}\) (EB . DE = AE . EC)
=> Tam giác EDA ~ Tam giác ECB (c - g - c)
=> ADE = BCE = 450 (tam giác ABC vuông cân tại A)