Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

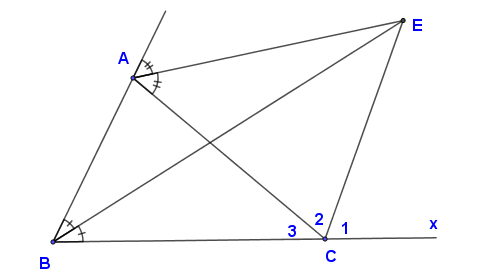
▶▸ Ta có: BEBE là tia phân giác góc BB (giả thiết)
AEAE là tia phân giác góc ngoài tại đỉnh AA (giả thiết)
⇒⇒ CECE là tia phân giác góc ngoài tại đỉnh CC (định lý bổ sung)
▶▸ Trên tia đối của tia CBCB vẽ tia CxCx
Khi đó ACxˆACx^ và C3ˆC3^ là hai góc kề bù
⇒⇒ ACxˆ=180o−C3ˆ=180o−30o=150oACx^=180o−C3^=180o−30o=150o
Vì CECE là tia phân giác của ACxˆACx^ ⇒⇒ C1ˆ=C2ˆ=ACxˆ2=150o2=75oC1^=C2^=ACx^2=150o2=75o
⇒⇒ BCEˆ=C3ˆ+C2ˆ=30o+75o=105oBCE^=C3^+C2^=30o+75o=105o

Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
75 độ