Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
hay \(AF\cdot AB=AE\cdot AC\)
b: Ta có: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
hay \(AF\cdot AB=AE\cdot AC\)
b: Ta có: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔABC

a: Xet ΔAFB vuông tại F và ΔAEC vuông tại E có
góc A chung
=>ΔAFB đồng dạng với ΔAEC
b: ΔAFB đồng dạng với ΔAEC
=>AF/AE=AB/AC
=>AF*AC=AB*AE
=>AF/AB=AE/AC
=>ΔAFE đồng dạng với ΔABC
c: Xét ΔBDH vuông tại D và ΔBFC vuông tại Fco
góc DBH chung
=>ΔBDH đồng dạng với ΔBFC

Sửa đề: ΔABC vuông tại A
a) Xét ΔDAB vuông tại D và ΔACB vuông tại A có
\(\widehat{ABC}\) chung
Do đó: ΔDAB\(\sim\)ΔACB(g-g)
b) Xét ΔABC có
BE là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\)(Định lí đường phân giác của tam giác)(1)
Ta có: ΔDAB\(\sim\)ΔACB(cmt)
nên \(\dfrac{AB}{BC}=\dfrac{BD}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(2)
Từ (1) và (2) suy ra \(\dfrac{AE}{EC}=\dfrac{BD}{AB}\)
hay \(AE\cdot AB=BD\cdot EC\)(đpcm)

a) xét \(\Delta ADB\)zà \(\Delta AEC\)có
\(\hept{\begin{cases}\widehat{A}chung\\\widehat{AEC}=\widehat{ADB}=90^0\end{cases}}\)
\(=>\Delta ADB~\Delta AEC\left(g.g\right)\)
\(=>\frac{AD}{AE}=\frac{AB}{AC}=>AD.AC=AB.AE\left(dpcm\right)\)
\(taco\left(\frac{AD}{AE}=\frac{AB}{AC}=>\frac{AD}{AB}=\frac{AE}{AC}\right)\)
xét \(\Delta ADE\)zà \(\Delta ABCco\)
\(\hept{\begin{cases}\widehat{A}chung\\\frac{AD}{AB}=\frac{AE}{AC}\end{cases}=>\Delta ABE~\Delta ABC\left(c.g.c\right)}\)
=>\(\widehat{ADE}=\widehat{ABC}\left(dpcm\right)\)
c) Xét tam giác AEC zà tam giác HDC óc
góc AEC= góc HDC =90 độ
góc HCE chung
=> tam giác AEC~ tam giác HDC
=>\(\frac{AC}{HC}=\frac{EC}{DC}=>AC.DC=EC.HC\left(1\right)\)
xét tam giác BEC zà tam giác HEA có
góc BEC= góc AEH= 90 độ
góc BCE = góc EAH ( cùng phụ zới góc EBC )
=> tam giác BEC ~ tam giác HEA (g.g)
=>\(\frac{BE}{HE}=\frac{EC}{EA}=>BE.EA=EC.HE\left(2\right)\)
từ 1 zà 2 suy ra
\(BE.BA+CD.CA=BH.BD+CH.CE\)
kẻ AH zuông goc zới BC cắt BC tại F
Tự CM \(\hept{\begin{cases}\Delta CFH~\Delta CEB\\\Delta BFH~\Delta BDC\end{cases}=>\hept{\begin{cases}CF.CB=CH.CE\\BF.BC=BH.BD\end{cases}=>BE.BA+CD.CA=CF.CB+BF.CB}}\)
\(=BC.\left(CF+BF\right)=BC^2\)
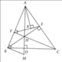

a: Xét ΔHEB vuông tại E và ΔHFC vuông tại F có
\(\widehat{EHB}=\widehat{FHC}\)(hai góc đối đỉnh)
Do đó: ΔHEB~ΔHFC
b: Xét ΔAEH vuông tại E và ΔADB vuông tại D có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔADB
=>\(\dfrac{AE}{AD}=\dfrac{AH}{AB}\)
=>\(AE\cdot AB=AH\cdot AD\)
c: Xét ΔAFB vuông tại F và ΔAEC vuông tại E có
\(\widehat{FAB}\) chung
Do đó: ΔAFB~ΔAEC
=>\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
Xét ΔAFE và ΔABC có
\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAFE~ΔABC