Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì HN\(\perp\)AC
HM \(\perp\)AB
Gọi O là giao điểm MN và HA
=> HMA = MAN = HMA = 90°
Xét tứ giác MHNA ta có :
HMA = MAN = HMA = 90°
=> MHNA là hình chữ nhật
=> MH = AN ( tính chất)
=> HMA = MAN = HMA = MHN = 90°
Mà AH\(\perp\)BC
Mà ta thấy :
MHA + AHN = MHN = 90°
CHN + AHN = AHC = 90°
=> MHA = NHC ( cùng phụ với AHN )
=> MHA = NHC = AHN
Xét ∆AHC có :
HN là phân giác ( AHN = CHN )
HN \(\perp\)AC
AHC = 90°
=> ∆AHC vuông cân tại H ( tính chất)
=> HN là trung tuyến ∆ vuông cân AHC
=> HN = AN = NC ( tính chất đường truyến trong ∆ vuông)
Mà MH = AN (cmt)
=> MH = HN
=> ∆MHN cân tại H
Xét ∆MHN ta có :
Mà HA là phân giác ( MHA = NHA )
=> HA là đường cao vừa là trung tuyến
=> HA \(\perp\)MN
Hay HO\(\perp\)MN
=> HON = 90°
Mà CHA = 90° (AH \(\perp\)BC )
=> HON = CHA = 90°
Mà 2 góc này ở vị trí đồng vị
=> BC//MN
=> ABC = NMA ( đồng vị)

A B C H D
Bài làm:
a) Xét 2 tam giác: \(\Delta ABC\)và \(\Delta HBA\)có:
\(\hept{\begin{cases}\widehat{ABC}chung\\\widehat{AHB}=\widehat{BAC}=90^0\end{cases}}\)
=> \(\Delta ABC\)đồng dang với \(\Delta HBA\)(G.G)
b) \(\Delta AHB\)đồng dạng với \(\Delta CAB\)(G.G) vì:
\(\hept{\begin{cases}\widehat{AHB}=\widehat{AHC}=90^0\\\widehat{BAH}=\widehat{ACH}=90^0-\widehat{HAC}\end{cases}}\)
=> \(\frac{BH}{AH}=\frac{AH}{HC}\)\(\Leftrightarrow AH^2=BH.HC\)
c) Vì tam giác ABC vuông tại A nên theo định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
Theo phần a, \(\Delta ABC\)đồng dạng với \(\Delta HBA\)(G.G)
=> \(\frac{BA}{AH}=\frac{BC}{AC}\Rightarrow AH=\frac{AB.AC}{BC}=\frac{48}{10}=4.8\left(cm\right)\)
Mà theo phần b, \(AH^2=BH.HC\)\(\Leftrightarrow BH.HC=4.8^2=23.04\Leftrightarrow HC=\frac{23.04}{HB}\)
Thay vào ta có: \(HB+HC=BC\)
\(\Leftrightarrow HB+\frac{23.04}{HB}=10\)
Từ đó ta giải phương trình ẩn HB ra, \(HB=3.6\left(cm\right)\)
=> \(HC=10-3.6=6.4\left(cm\right)\)
d) Đề bạn viết nhầm phải là cho AD là phân giác của tam giác ABC.
Áp dụng tính chất của tia phân giác trong tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}\Leftrightarrow DC=\frac{4}{3}BD\)
Thay vào đó, ta giải phương trình sau:
\(BD+DC=BC\Leftrightarrow BD+\frac{4}{3}BD=10\)
Từ đó ta giải phương trình ẩn BD => \(BD=\frac{30}{7}cm\)
=> Diện tích tam giác ABD là:
\(S\Delta ABD=\frac{AH.BD}{2}=\frac{4.8\times\frac{30}{7}}{2}=\frac{72}{7}\left(cm^2\right)\)
Học tốt!!!!


k mk đi
mk k lại
thanks
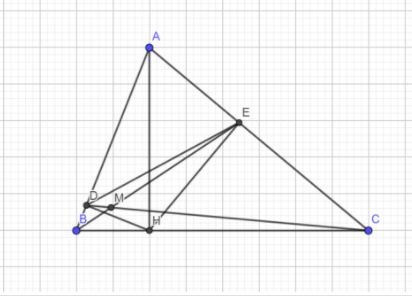
A B C H D E
Vi HD va HE lan luot la hinh chieu cua tam giac ABC nen
HD vuong goc voi AB
HE vuong goc voi AC
xet 2 tam giac ABH va tam giac AHD
co: goc BAH: chung
goc ADH = goc AHB = 90 do
Do do : tam giac ABH dong dang voi tam giac AHD (g-g)