Question

[Sleepy Ash Kuro]

Cho ΔABC cân tại A. Kẻ BD ⊥ AC. Lấy điểm E bất kỳ trên cạnh BC (E khác B, C). Kẻ EF, EG, EH lần lượt vuông góc với AB, AC, BD. Cm:

a) ΔHBE = ΔFEB

b) EF + EG = BD

c) Trên tia đối của tia CA lấy điểm K sao cho KC = BF; BC cắt FK tại I. Cm: I là trung điểm của FK

d) Nêu cách xác định điểm E trên BC để ΔEGH vuông cân

Answer 1

[Vũ Minh Tuấn]

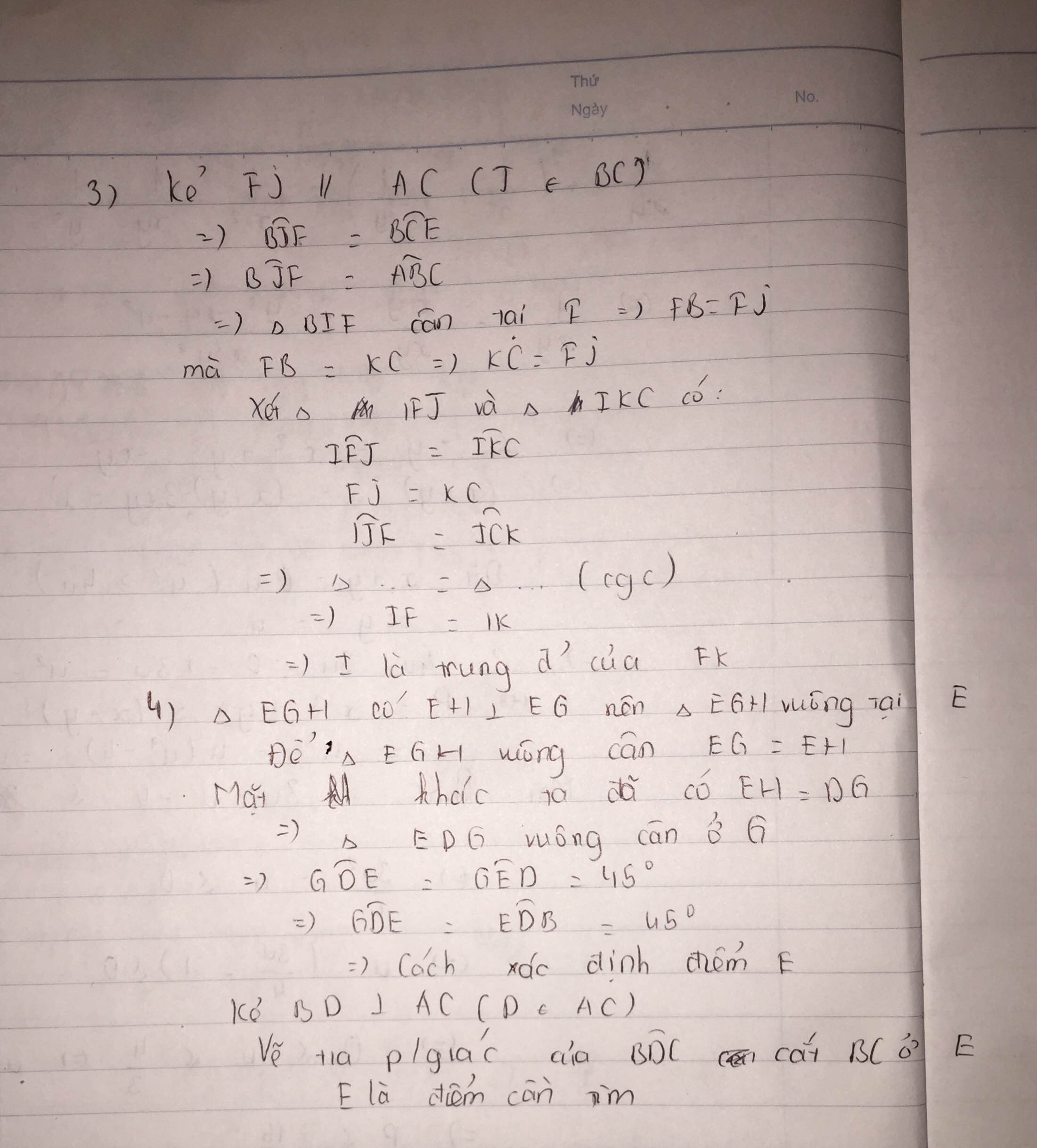
a) Vì:

\(\left\{{}\begin{matrix}AC\perp BD\left(gt\right)\\EH\perp BD\left(gt\right)\end{matrix}\right.\)

=> \(AC\) // \(EH\) (từ vuông góc đến song song).

=> \(\widehat{ACB}=\widehat{HEB}\) (vì 2 góc đồng vị).

+ Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)

=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất tam giác cân).

Mà \(\widehat{ACB}=\widehat{HEB}\left(cmt\right)\)

=> \(\widehat{ABC}=\widehat{HEB}.\)

Hay \(\widehat{FBE}=\widehat{HEB}.\)

Xét 2 \(\Delta\) vuông \(HBE\) và \(FEB\) có:

\(\widehat{BHE}=\widehat{EFB}=90^0\left(gt\right)\)

Cạnh BE chung

\(\widehat{HEB}=\widehat{FBE}\left(cmt\right)\)

=> \(\Delta HBE=\Delta FEB\) (cạnh huyền - góc nhọn).

b) Theo câu a) ta có \(\Delta HBE=\Delta FEB.\)

=> \(BH=EF\) (2 cạnh tương ứng) (1).

+ Vì:

\(\left\{{}\begin{matrix}BD\perp AC\left(gt\right)\\EG\perp AC\left(gt\right)\end{matrix}\right.\)

=> \(BD\) // \(EG\) (từ vuông góc đến song song).

Hay \(HD\) // \(EG\)

+ Vì \(AC\) // \(EH\left(cmt\right)\)

=> \(DG\) // \(EH\)

Mà \(HD\) // \(EG\left(cmt\right)\)

=> \(HD=EG\) (theo tính chất đoạn chắn) (2).

Từ (1) và (2) => \(EF+EG=BH+HD\)

Mà \(BH+HD=BD\left(gt\right)\)

=> \(EF+EG=BD.\)

c) Từ F kẻ \(FJ\) // \(AC\) \(\left(J\in BC\right).\)

=> \(\widehat{FJB}=\widehat{ACB}\) (vì 2 góc so le trong).

Mà \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)

=> \(\widehat{FJB}=\widehat{ABC}.\)

Hay \(\widehat{FJB}=\widehat{FBJ}.\)

=> \(\Delta BJF\) cân tại \(F.\)

=> \(FB=FJ\) (tính chất tam giác cân).

Mà \(FB=KC\left(gt\right)\)

=> \(FJ=KC.\)

+ Vì \(FJ\) // \(AC\) (do cách vẽ).

=> \(FJ\) // \(KC.\)

=> \(\left\{{}\begin{matrix}\widehat{IFJ}=\widehat{IKC}\\\widehat{FJI}=\widehat{KCI}\end{matrix}\right.\) (vì các góc so le trong).

Xét 2 \(\Delta\) \(IFJ\) và \(IKC\) có:

\(\widehat{IFJ}=\widehat{IKC}\left(cmt\right)\)

\(FJ=KC\left(cmt\right)\)

\(\widehat{FJI}=\widehat{KCI}\left(cmt\right)\)

=> \(\Delta IFJ=\Delta IKC\left(g-c-g\right)\)

=> \(IF=IK\) (2 cạnh tương ứng).

=> \(I\) là trung điểm của \(FK\left(đpcm\right).\)

Chúc bạn học tốt!