Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

. Bán kính đường tròn ngoại tiếp tam giác ABC có độ dài bằng 15
=>AO=OB=OC=15
xét tam giác AHO vuông tai H
=>HO=căn(15^2-14.4^2)=4.2
=>BH =BO-HO=15-4.2=10.8
Xét tam giác ABH vuông tại H
=>AB=căn(14.4^2+10.8^2)=18
=>BC=2OC=2*15=30
=>AC=căn(30^2-18^2)=24
=>AB+AC=18+24=42

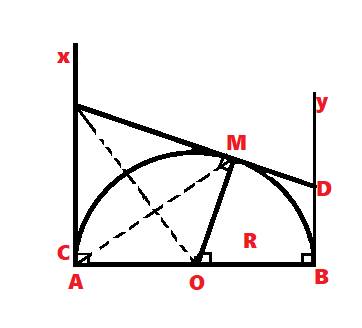
a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của \(\widehat{MOA}\)
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
CA=CM
=>C nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
b: Xét tứ giác CAOM có \(\widehat{CAO}+\widehat{CMO}=90^0+90^0=180^0\)
nên CAOM là tứ giác nội tiếp
=>C,A,O,M cùng thuộc một đường tròn
c: Xét (O) có
DM,DB là tiếp tuyến
Do đó: OD là phân giác của góc MOB và DM=DB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>ΔCOD vuông tại O
Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
mà MC=CA và DM=DB
nên \(CA\cdot DB=OM^2=R^2\)



A B C H O x
Gọi đường tròn ngoại tiếp tam giác ABC là (O;x cm)
(Đặt độ dài bán kính của (O) là x cm)
Ta có : CH = 1/2BC = 6 (cm)
Dễ dàng c/m được ba điểm A,H,O thẳng hàng => OH = x - 4 (cm)
Áp dụng đ/l Pytago : \(HC^2+OH^2=OC^2\Leftrightarrow\left(x-4\right)^2+6^2=x^2\Leftrightarrow4x=52\Leftrightarrow x=13\)
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 13 cm
Vì AH là đường cao => BH=HC=BC/2=6 cm
Áp dụng đ/lý Pi ta go vào tam giác ABH ta được:
\(AB^2=AH^2+BH^2\)
\(AB^2=4^2+6^2=52=\left(2\sqrt{13}\right)^2\)
=> \(AB=2\sqrt{13}\)
=> \(AC=2\sqrt{13}\)
=> Bán kính đường tròn ngoại tiếp tam giác cân ABC là:
\(R=\frac{2\sqrt{13}.2\sqrt{13}.12}{4.S}=\frac{624}{4.24}=\frac{13.2.24}{4.2.24}=\frac{13}{4}\)(cm)