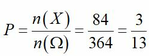Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
*Đa giác lồi (H) có 22 cạnh nên cũng có 22 đỉnh. Số tam giác có 3 đỉnh là đỉnh của đa giác (H) là C 22 3 = 1540 (tam giác)
Suy ra số phàn tử của không gian mẫu Ω là n ( Ω ) = C 1540 2 .
*Số tam giác của một cạnh là cạnh của đa giác (H) là 22.18 = 396 (tam giác).
Số tam giác có hai cạnh là cạnh của đa giác (H) là 22 (tam giác)
Số tam giác không có cạnh nào là cạnh của đa giác (H) là:
1540 – 396 – 22 = 1122 (tam giác).
Gọi A là biến cố “Hai tam giác được chọn có 1 cạnh là cạnh của đa giác (H) và 1 tam giác không có cạnh nào là cạnh của đa giác (H)”
Số phần tử của A là n ( A ) = C 396 1 . C 1122 1 .
*Vậy xác suất cần tìm là
P ( A ) = n ( A ) n ( Ω ) = C 396 1 . C 1122 1 C 1540 2 = 748 1995 ≈ 0,375.

Cho đa giác đều có 15 đỉnh. Gọi M là tập hợp các tam giác có ba đỉnh là ba đỉnh của đa giác đã cho. Chọn ngẫu nhiên một tam giác thuộc M, tính xác suất để tam giác được chọn là tam giác cân nhưng không phải là tam giác đều
A. 3/91
B. 18/91
C. 3/13
D. 1/26

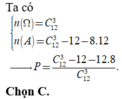
Thật vậy:
• Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
• Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác. (hoặc hiểu theo cách khác: tam giác có 3 đỉnh là 3 đỉnh liên tiếp của đa giác tức là có 2 cạnh là 2 cạnh liên tiếp của đa giác, 2 cạnh này cắt nhau tại 1 đỉnh, mà đa giác này có 12 đỉnh nên có 12 tam giác thỏa trường hợp này)
• Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: Trước tiên ta chọn 1 cạnh trong 12 cạnh của đa giác nên có 12 cách chọn; tiếp theo chọn 1 đỉnh còn lại trong 8 đỉnh (trừ 2 đỉnh tạo nên cạnh đã chọn và 2 đỉnh liền kề với cạnh đã chọn). Do đó trong trường hợp này có 8.12 tam giác.

Đáp án B
Số phần tử của tập hợp M là: C 15 3
Gọi O là tâm đường tròn ngoại tiếp của đa giác đều, Xét một đỉnh A bất kỳ của đa giác: Có 7 cặp đỉnh của đa giác đối xứng với nhau qua đường thẳng OA, hay có 7 tam giác cân tại đỉnh A. Như vậy, với mỗi một đỉnh của đa giác có 7 tam giác nhận nó làm đỉnh tam giác cân.
Số tam giác đều có 3 đỉnh là các đỉnh của đa giác là 15 3 = 5 tam giác.
Tuy nhiên, trong các tam giác cân đã xác định ở trên có cả tam giác đều, do mọi tam giác đều thì đều cân tại 3 đỉnh nên tam giác đều được đếm 3 lần.
Suy ra, số tam giác cân nhưng không phải tam giác đều có 3 đỉnh là 3 đỉnh của đa giác đã cho là: 7.15 − 3.5 = 90
Do đó xác suất cần tìm là P = 90 C 15 3 = 18 91

HD: Chọn ra 3 đỉnh bất kỳ của đa giác có: C 10 3 cách chọn.
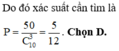
■ Số tam giác có 2 cạnh là cạnh của đa giác là: 10
(vì ứng với mỗi đỉnh ta lấy 2 cạnh kề với nó là được tgiác như điều kiện đã xét)
■ Số tam giác có 1 cạnh là cạnh của đa giác là: 10.6 = 60 vì chọn 1 cạnh của đa giác, ta chọn được 6 đỉnh để tạo tam giác (trừ đi 2 đỉnh của cạnh đó và 2 đỉnh nằm kề sát cạnh đó), mà có 10 cạnh như thế nên có 10.6 = 60
Suy ra số tgiác được tạo thành từ các đường chéo của đa giác là: 120 - 10 - 60 = 50 tam giác.
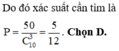

Đáp án C
+) Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: cứ 1 cạnh, trừ đi 2 đỉnh kể, còn 8 đỉnh, với 2 đỉnh đầu mút của cạnh đó cho 1 tam giác thỏa mãn đề bài, nên có 8.12 tam giác
Vậy số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh nào là cạnh của đa giác là C 12 3 − 12 − 8.12
Vậy kết quả là C 12 3 − 12 − 8.12 C 12 3

Số phần tử của tập X là C 4 n 3
Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O.
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4n-2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
Từ giả thiết suy ra P A = C 2 n 1 . C 4 n - 2 1 C 4 n 3 = 1 13 ⇒ n = 10
Đáp án C

Chọn D.
Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác => có C 14 3 = 364 cách.
Suy ra số phần tử của không gian mẫu là n Ω = 364 .
Gọi X là biến cố “3 đỉnh được chọn là 3 đỉnh của một tam giác vuông”
Gọi O là tâm đường tròn ngoại tiếp đa giác đều => có 7 đường kính đi qua O.
Xét một đường kính bất kì, mỗi đỉnh còn lại sẽ tạo với đường kính một tam giác vuông.
Khi đó, số tam giác vuông được tạo ra là 7.(6+6)=84=>n(X)=84.
Vậy xác suất cần tính là