Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là C n 2 , trong đó có n cạnh, suy ra số đường chéo là C n 2 - n
+ Đa giác đã cho có 135 đường chéo nên C n 2 − n = 135
+ Giải phương trình
n ! n − 2 ! 2 ! = 135 , n ∈ ℕ , n ≥ 2 ⇔ n − 1 n − 2 n = 270 ⇔ n 2 − 3 n − 270 = 0 ⇔ n = 18 n h a n n = − 15 l o a i ⇔ n = 18

Chọn C
Với hai đỉnh sẽ cho ta một đoạn thẳng, do đó số đoạn thẳng được tạo ra từ n đỉnh là C n 2
Đa giác có n đỉnh sẽ có n cạnh. Trong số C n 2 đoạn thẳng có n đoạn thẳng là cạnh của đa giác. Do đó số đường chéo của đa giác là
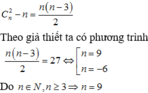

Đáp án B
Ta sắp xếp các cạnh giá trị u 1 ; … u n tăng dần theo cấp số cộng là 3. Khi đó ta có:
S n = 158 u n = 44 ⇔ u 1 + 44 . n 2 = 158 u 1 + 3 n − 1 = 44 ⇔ u 1 = 47 − 3 n 47 − 3 n + 44 . n = 316 *
* ⇔ 3 n 2 − 91 n + 316 = 0 ⇔ n = 4 T M n = 79 3 L

Đáp án D
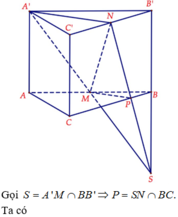
Số tam giác tạo thành khi chọn ngẫu nhiên 3 điểm là: C 2 n 3
Số đường chéo đi qua tâm là n ⇒ số hình chữ nhật nhận 2 đường chéo đi qua tâm làm 2 đường chéo là: C n 2
Số tam giác vuông được tạo thành là 4 C n 2
Ta có: 4 C n 2 C 2 n 3 = 1 5 ⇒ n = 8.
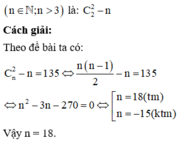
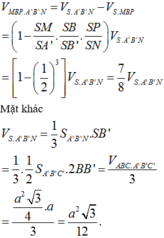
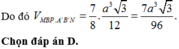


Đáp án A
Phương pháp
Tìm số cạnh và số đường chéo của đa giác đều n cạnh.
Cách giải
Khi nối hai đỉnh bất kì của đa giác ta được một số đoạn thẳng, trong đó bao gồm cạnh của đa giác và đường chéo của đa giác đó.
Đa giác đều n cạnh có n đỉnh, do đó số đường chéo là C n 2 − n
Theo giả thiết bài toán ta có
C n 2 − n = n ⇔ C n 2 = 2 n ⇔ n ! 2 ! n − 2 ! = 2 n ⇔ n n − 1 = 4 n ⇔ n − 1 = 4 ⇔ n = 5