Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
Ta có: u 4 = - 12 u 14 = 18
⇔ u 1 + 3 d = - 12 u 1 + 13 d = 18
⇔ u 1 = - 21 d = 3
Tổng của 16 số hạng đầu tiên của cấp số cộng là:
S 16 = 16 . ( - 21 ) + 16 . 15 2 . 3 = 24

\(\left\{{}\begin{matrix}u1+u2+u3=13\\u4-u1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q+u_1\cdot q^2=13\\u_1\cdot q^3-u_1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1+q+q^2}{\left(q-1\right)\left(q^2+q+1\right)}=\dfrac{13}{26}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{q-1}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}q-1=2\\u_1=\dfrac{26}{q^3-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}q=2+1=3\\u_1=\dfrac{26}{3^3-1}=1\end{matrix}\right.\)
Tổng 8 số hạng đầu của cấp số nhân là:
\(\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1\cdot\left(1-3^8\right)}{1-3}=3280\)
\(\left\{{}\begin{matrix}u_1+u_2+u_3=13\\u_4-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1+u_1.q+u_1.q^2=13\\u_1.q^3-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q-1\right)\left(q^2+q+1\right)=26\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13.\left(q-1\right)=26\\u_1.\left(q^3-1\right)=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}q=3\\u_1=1\end{matrix}\right.\)
\(S_8=\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1.\left(1-3^8\right)}{1-3}=3280\)

Ta có: u 2 + u 8 + u 9 + u 15 = 100
⇔ u 1 + d + u 1 + 7 d + u 1 + 8 d + u 1 + 14 d = 100 ⇔ 4 u 1 + 30 d = 100 ⇔ 2 u 1 + 15 d = 50.
Khi đó S 16 = 16 2 2 u 1 + 15 d = 8.50 = 400
Chọn đáp án D.

Chọn D.
Gọi d là công sai của cấp số đã cho
Ta có: S100 = 50(2u1 +99d) = 24850 ⇒ ![]()
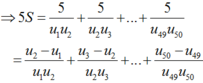
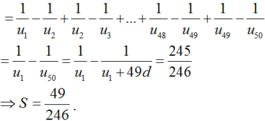

\(\left\{{}\begin{matrix}u_1+d=3\\u_1+9d=-15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=\dfrac{21}{4}\\d=-\dfrac{9}{4}\end{matrix}\right.\)
\(S_{20}=\dfrac{21}{4}.20+\dfrac{19.20}{2}.\left(-\dfrac{9}{4}\right)=-\dfrac{645}{2}\)

Gọi d là công sai.
Ta có: \(U_4=U_1+3d\)
\(U_{97}=U_1+96d\)
=> \(U_4+U_{97}=101\)
=> \(U_1+3d+U_1+96d=101\)
=> \(U_1+U_1+99d=101\)
=> \(U_1+U_{100}=101\)
Tổng 100 số hạng đầu là: \(\frac{U_{100}+U_1}{2}.100=\frac{101.100}{2}=\)5050