
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


MIk gửi link ảnh rồi
k mik nha
Chỉ cần thay chữ vào thôi

có 1 người. Ba kẻ mù - bố kẻ mù. không chạy ngang, sau, trước vì có 1 người


TA CÓ AM LÀ TRUNG TUYẾN CỦA BC MÀ BC=CM+BM=>CM=BM=5CM
XÉT TAM GIÁC AMB VUÔNG TẠI M ;ÁP DỤNG ĐL PYTAGO TA CÓ
MA^2+MB^2=AB^2
=>AM^2=AB^2-BM^2
=>AM^2=13^2-10^2
=>AM^2=69
=>AM=\(\sqrt{69}\)
B,

A B H E C D I
Từ D hạ DI vuông góc với AH sao cho I thuộc AH => Góc AID = 90 độ
Xét tam giác vuông ABH và tam giác vuông DIA có: AB=AD (gt),
\(\widehat{A_1}+\widehat{A_2}=90^o\) mà \(\widehat{A_2}+\widehat{D_1}=90^o\) => \(\widehat{A_1}=\widehat{D_1}\) , \(\widehat{AID}=\widehat{AHB}=90^o\)
=> Tam giác AHB= tam giác DIA (ch-gn) => AH=DI (1)
Xét tứ giác IHDE có : \(\widehat{HID}=\widehat{IHE}=\widehat{HED}=90^o\) => Tứ giác IHED là hình chữ nhật => HE=DI (2)
Từ (1) và (2) => HA=HE => đpcm
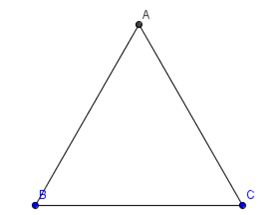 cân tại A kẻ AK
cân tại A kẻ AK 


