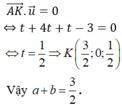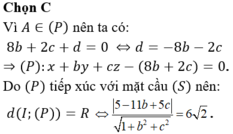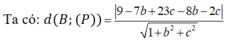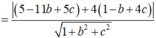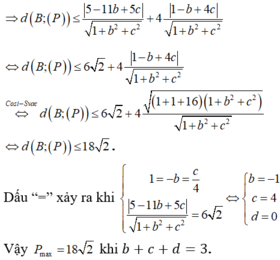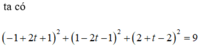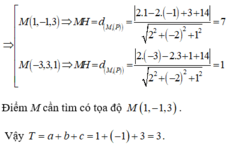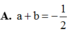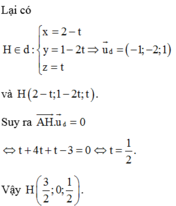Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Mặt phẳng cần tìm sẽ vuông góc với (ABM). Một vecto pháp tuyến của nó là tích có hướng của vecto pháp tuyến mặt phẳng (ABM) và A B →
Cũng có thể làm như sau: Khoảng cách lớn nhất là MH với H là hình chiếu vuông góc của M lên đường thẳng AB. Ta tìm được H(3;-3;-10)
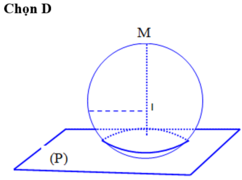
Mặt (S) cầu có tâm I (1;2;3), R=3.
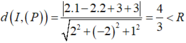mặt phẳng cắt mặt cầu theo một đường tròn
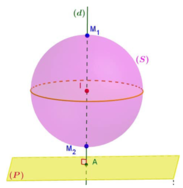
Gọi M (a;b;c) là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nhất.
Khi M thuộc đường thẳng Δ vuông đi qua M và vuông góc với (P)
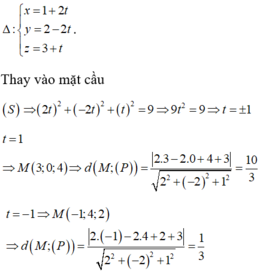
Vậy M (3;0;4) a + b + c = 7.
Chọn D
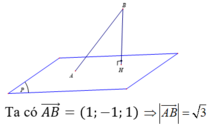
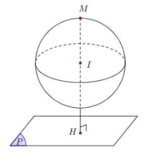
Gọi H là hình chiếu của B trên mặt phẳng (P) khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P). Ta luôn có BH ≤ AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A, khi đó 
là véc tơ pháp tuyến của mặt phẳng (P)
Vậy phương trình mặt phẳng (P) đi qua A (-1; 2; 4) và có véc tơ pháp tuyến 
là x - y + z - 1 = 0
Vậy khoảng cách từ điểm O đến mặt phẳng (P) là:
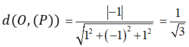
Đáp án C
Phương trình đường thẳng IH
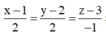
Độ dài MH lớn nhất => M là một trong hai giao điểm của MI và (S)
Suy ra MI ≡ MH, gọi M(1+2t;2+2t;3-t) ∈ (S)
Do đó
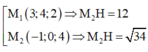
Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 ó m(y + 2z – 1) + x + z – 2 = 0 (*)
Phương trình (*) có nghiệm với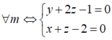 
Suy ra (P) luôn đi qua đường thẳng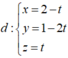 
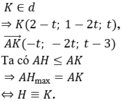
Đường thẳng d có VTCP 
