Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P\left(x\right)-Q\left(x\right)=\left(-2x+\frac{1}{2}x^2+3x^4-3x^2-3\right)-\left(3x^4+x^3-4x^2+1,5x^3-3x^4+2x+1\right)\\ P\left(x\right)-Q\left(x\right)=-2x+\frac{1}{2}x^2+3x^4-3x^2-3-3x^4-x^3+4x^2-1,5x^3+3x^4-2x-1\\ P\left(x\right)-Q\left(x\right)=\left(-2x-2x\right)+\left(\frac{1}{2}x^2-3x^2+4x^2\right)+\left(3x^4-3x^4+3x^4\right)+\left(-3-1\right)+\left(-x^3-1,5x^3\right)\\ P\left(x\right)-Q\left(x\right)=-4x+\frac{3}{2}x^2+3x^4-4-\frac{5}{2}x^3\)
\(R\left(x\right)+P\left(x\right)-Q\left(x\right)+x^2=2x^3-\frac{3}{2}x+1\\ \Rightarrow R\left(x\right)+\left(P\left(x\right)-Q\left(x\right)\right)+x^2=2x^3-\frac{3}{2}x+1\\ \Rightarrow R\left(x\right)-4x+\frac{3}{2}x^2+3x^4-4-\frac{5}{2}x^3+x^2=2x^3-\frac{3}{2}x+1\\ \Rightarrow R\left(x\right)-4x+\left(\frac{3}{2}x+x^2\right)+3x^4-4-\frac{5}{2}x^3=2x^3-\frac{3}{2}x+1\\ \Rightarrow R\left(x\right)-4x+\frac{5}{2}x^2+3x^4-4-\frac{5}{2}x^3=2x^3-\frac{3}{2}x+1\\ \Rightarrow R\left(x\right)=2x^3-\frac{3}{2}x+1+4x-\frac{5}{2}x^2-3x^4+4+\frac{5}{2}x^3\\ \Rightarrow R\left(x\right)=\left(2x^3+\frac{5}{2}x^3\right)+\left(\frac{-3}{2}x+4x\right)+\left(1+4\right)-\frac{5}{2}x^2-3x^4\\ \Rightarrow R\left(x\right)=\frac{9}{2}x^3+\frac{5}{2}x+5-\frac{5}{2}x^2-3x^4\)

Ta có: \(F\left(x\right)+G\left(x\right)-H\left(x\right)=0\)
\(\Leftrightarrow4x^2+3x-2+3x^2-2x+5-5x^2+2x-3=0\\ \Leftrightarrow2x^2+3x=0\\ \Rightarrow x\left(2x+3\right)=0\\ \Rightarrow x=0;x=\dfrac{-3}{2}\)
Vậy tìm được x thỏa mãn là: \(x=0;x=\dfrac{-3}{2}\)

\(f\left(x\right)+h\left(x\right)-g\left(x\right)\)
\(=\left(5x^4+3x^2+x-1\right)+\left(-x^4+3x^3-2x^2-x+2\right)\)
\(-\left(2x^4-x^3+x^2+2x+1\right)\)
\(=\left(5x^4-x^4-2x^4\right)+\left(3x^3+x^3\right)+\left(3x^2-2x^2-x^2\right)\)
\(+\left(x-x-2x\right)+\left(-1+2-1\right)\)
\(=2x^4+4x^3-2x\)

P (x) = x5 + 2x4 + x2 - x +1
Q (x) = 6 - 2x + 3x3 + x4 - 3x5
P (x) - Q (x) = (x5 + 2x4 + x2 - x +1) - ( 6 - 2x + 3x3 + x4 - 3x5)
= x5 + 2x4 + x2 - x +1 - 6 + 2x - 3x3 - x4 + 3x5
= ( x5 + 3x5 ) + ( 2x4 - x4 ) - 3x3 + x2 + ( -x + 2x ) +( 1 - 6 )
= 4x5 + x4 - 3x3 + x2 + x - 5
Q (x) - P (x) = ( 6 - 2x + 3x3 + x4 - 3x5 ) - (x5 + 2x4 + x2 - x +1)
= 6 - 2x + 3x3 + x4 - 3x5 - x5 - 2x4 - x2 + x -1
= - ( 3x5 + x5 ) + ( x4 - 2x4 ) + 3x3 - x2 - ( 2x - x ) + ( 6 - 1)
= - 4x5 - x4 + 3x3 - x2 - x + 5
* Nhận xét: Hệ số của hai đa thức P (x) và Q(x) đối nhau.

a) B(x)=\(4x^5\) -\(2x^4\) +\(3x^3\) -\(2x^2\) +\(4x\) +\(\dfrac{-1}{2}\)
b) C(x)=\(2x^4-x^3+\dfrac{1}{2}+4x\)

Ta có: P(x) = x4 - 3x2 + 1212 – x.
a) Vì P(x) + Q(x) = x5 – 2x2 + 1 nên
Q(x) = x5 – 2x2 + 1 - P(x)
Q(x) = x5 – 2x2 + 1 - x4 + 3x2 - 1212 + x
Q(x) = x5 - x4 + x2 + x + 1212
b) Vì P(x) - R(x) = x3 nên
R(x) = x4 - 3x2 + 1212 – x - x3
hay R(x) = x4 - x3 - 3x2 – x + 1212.

Ta có : \(A\left(x\right)+C\left(x\right)=3-2x^3-x+x^2-4x^2-3x^2-2x^3+3x-2\)
\(=-4x^3-6x^2+2x+1\)
\(A\left(x\right)-B\left(x\right)=3-2x^3-x+x^2-4x^2-\left(-x^3+9x^2-8x-5-2x^2\right)\)
\(=3-2x^3-x+x^2-4x^2+x^3-9x^2+8x+5+2x^2\)
\(=-x^3-10x^2+7x+8\)

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
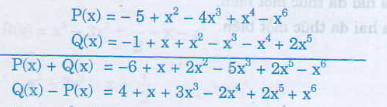 .
.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
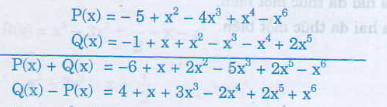
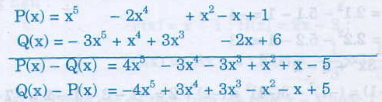
Rút gọn:
\(P\left(x\right)=2x^2+4x\)
\(Q\left(x\right)=-x^3+2x^2-x+2\)
Để \(R\left(x\right)-P\left(x\right)-Q\left(x\right)=0\)
<=> \(R\left(x\right)=P\left(x\right)+Q\left(x\right)\)
= \(\left(2x^2+4x\right)+\left(-x^3+2x^2-x+2\right)\)
= \(-x^3+4x^2+3x+2\)
KL: \(R\left(x\right)=-x^3+4x^2+3x+2\)