Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(d\left(C;d\right)=\frac{\left|3.2-4\left(-5\right)+4\right|}{\sqrt{3^2+4^2}}=6\)
\(S_{ABC}=\frac{1}{2}AB.d\left(C;d\right)=\frac{1}{2}AB.6=15\Rightarrow AB=5\)
Gọi \(A\left(a;\frac{3a+4}{4}\right)\) \(\Rightarrow\overrightarrow{AI}=\left(a-2;\frac{3a-6}{4}\right)\Rightarrow AI=\sqrt{\left(a-2\right)^2+\left(\frac{3a-6}{4}\right)^2}=\frac{5}{2}\left|a-2\right|\)
\(AB=2IA\Rightarrow AI=\frac{5}{2}\Rightarrow\left|a-2\right|=1\Rightarrow\left[{}\begin{matrix}a=3\\a=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}A\left(3;\frac{13}{4}\right)\\B\left(1;\frac{7}{4}\right)\end{matrix}\right.\)

Đường thẳng \(\Delta\) nhận (3;-4) là 1 vtpt
a. Do \(d_1||\Delta\) nên \(d_1\) cũng nhận (3;-4) là 1 vtpt
Phương trình d1:
\(3\left(x-2\right)-4\left(y-5\right)=0\Leftrightarrow3x-4y+14=0\)
b. Do d2 vuông góc \(\Delta\) nên d2 nhận (4;3) là 1 vtpt
Phương trình d2:
\(4\left(x-2\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-23=0\)

1. Gọi d' là đường thẳng qua A và vuông góc d
\(\Rightarrow\) d' nhận (1;3) là 1 vtpt
Phương trình d':
\(1\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-4=0\)
H là giao điểm d và d' nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+3y-4=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{5}\\y=\dfrac{8}{5}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)
2.
Do A' đối xứng A qua d nên H là trung điểm AA'
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=\dfrac{2}{5}\\y_{A'}=2y_H-y_A=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow A'\left(\dfrac{2}{5};\dfrac{1}{5}\right)\)
3.
Gọi B là giao điểm d và \(\Delta\) thì tọa độ B thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow B\left(-\dfrac{3}{7};\dfrac{19}{7}\right)\)
Lấy điểm \(C\left(0;4\right)\) thuộc d
Phương trình đường thẳng \(d_1\) qua C và vuông góc \(\Delta\) có dạng:
\(2\left(x-0\right)-\left(y-4\right)=0\Leftrightarrow2x-y+4=0\)
Gọi D là giao điểm \(\Delta\) và \(d_1\Rightarrow\left\{{}\begin{matrix}x+2y-5=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow D\left(-\dfrac{3}{5};\dfrac{14}{5}\right)\)
Gọi D' là điểm đối xứng C qua \(\Delta\Rightarrow\) D là trung điểm CD'
\(\Rightarrow\left\{{}\begin{matrix}x_{D'}=2x_D-x_C=-\dfrac{6}{5}\\y_{D'}=2y_D-y_C=\dfrac{8}{5}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BD'}=\left(-\dfrac{27}{35};-\dfrac{39}{35}\right)=-\dfrac{3}{35}\left(9;13\right)\)
Phương trình đường thẳng đối xứng d qua denta (nhận \(\left(9;13\right)\) là 1 vtcp và đi qua D':
\(\left\{{}\begin{matrix}x=-\dfrac{6}{5}+9t\\y=\dfrac{8}{5}+13t\end{matrix}\right.\)

Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
a. Đường thẳng cắt đường tròn tại 2 điểm pb khi:
\(d\left(I;d\right)< R\Leftrightarrow\dfrac{\left|\sqrt{2}-2m+1-\sqrt{2}\right|}{\sqrt{2+m^2}}< 3\)
\(\Leftrightarrow\left(2m-1\right)^2< 9\left(m^2+2\right)\)
\(\Leftrightarrow8m^2+4m+17>0\) (luôn đúng)
Vậy đường thẳng luôn cắt đường tròn tại 2 điểm pb với mọi m
b. \(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\) do \(sin\widehat{AIB}\le1\)
Dấu "=" xảy ra khi \(sin\widehat{AIB}=1\Rightarrow\Delta IAB\) vuông cân tại I
\(\Rightarrow d\left(I;d\right)=\dfrac{R}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2m-1\right|}{\sqrt{m^2+2}}=\dfrac{3}{\sqrt{2}}\)
\(\Leftrightarrow m^2+8m+16=0\Rightarrow m=-4\)

Đáp án: B
d: x + 2y - 2 = 0 có 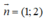
Gọi d’ là đường thẳng đi qua M và vuông góc với d 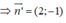
⇒ d': 2(x - 2) - (y - 5) = 0 ⇔ 2x - y + 1 = 0
Gọi I là giao điểm của d và d’. Suy ra, tọa độ của I là nghiệm của hệ phương trình:
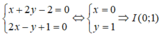
Vì M và M’ đối xứng nhau qua d nên I là trung điểm của MM’
⇒ M'(-2;-3)