Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(D=\dfrac{\left(2!\right)^2}{1^2}+\dfrac{\left(2!\right)^2}{3^2}+\dfrac{\left(2!\right)^2}{5^2}+...+\dfrac{\left(2!\right)^2}{2015^2}\)
\(D=\left(2!\right)^2\left(\dfrac{1}{3^2}+\dfrac{1}{5^2}+...+\dfrac{1}{2015^2}\right)\)
Xét số hạng tổng quát dạng: \(\dfrac{1}{\left(2n+1\right)^2}\) với \(n\in N\ge1\)
Ta có: \(\left(2n+1\right)^2-2n\left(2n+1\right)=1>0\)
\(\Rightarrow\left(2n+1\right)^2>2n\left(2n+1\right)\Rightarrow\dfrac{1}{\left(2n+1\right)^2}< \dfrac{1}{2n\left(2n+1\right)}\)
Do đó: \(\left\{{}\begin{matrix}\dfrac{1}{3^2}< \dfrac{1}{2.4}\\\dfrac{1}{5^2}< \dfrac{1}{4.6}\\....\\\dfrac{1}{2015^2}< \dfrac{1}{2014.2016}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}...+\dfrac{1}{2015^2}< 1+\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{2014.2016}\)
\(\Leftrightarrow\dfrac{D}{\left(2!\right)^2}< 1+\dfrac{1}{2.4}+\dfrac{1}{4.6}+..+\dfrac{1}{2014.2016}\)
\(\Leftrightarrow D< 4\left(1+\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{2014.2016}\right)\)
\(\Leftrightarrow D< 4+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{1007.1008}\)
\(\Leftrightarrow D< 4+\dfrac{2-1}{1.2}+\dfrac{3-2}{2.3}+...+\dfrac{1008-1007}{1007.1008}\)
\(\Leftrightarrow D< 4+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{...1}{1007}-\dfrac{1}{1008}\)
\(\Leftrightarrow D< 5-\dfrac{1}{1008}< 5< 6\)

\(D=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right)....\left(1-\dfrac{1}{2015}\right)\)
\(D=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{2014}{2015}=\dfrac{1.2.3....2014}{2.3.4....2015}\)
\(D=\dfrac{1}{2015}\)
\(D=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right)...\left(1-\dfrac{1}{2015}\right)\)
\(D=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{2014}{2015}=\dfrac{1.2.3...2014}{2.3.4...2015}\)
\(D=\dfrac{1}{2015}\)

a: \(=\dfrac{5\cdot\left(8-6\right)}{10}=\dfrac{5\cdot2}{10}=1\)
b: \(\dfrac{\left(-4\right)^2}{5}=\dfrac{16}{5}\)
\(B=\dfrac{3}{7}-\dfrac{1}{5}-\dfrac{3}{7}=-\dfrac{1}{5}\)
c: \(C=\left(6-2.8\right)\cdot\dfrac{25}{8}-\dfrac{8}{5}\cdot4\)
\(=\dfrac{16}{5}\cdot\dfrac{25}{8}-\dfrac{32}{5}\)
\(=5\cdot2-\dfrac{32}{5}=10-\dfrac{32}{5}=\dfrac{18}{5}\)
d: \(D=\left(\dfrac{-5}{24}+\dfrac{18}{24}+\dfrac{14}{24}\right):\dfrac{-17}{8}\)
\(=\dfrac{27}{24}\cdot\dfrac{-8}{17}=\dfrac{-9}{8}\cdot\dfrac{8}{17}=\dfrac{-9}{17}\)

a) \(\dfrac{\left(0,6\right)^5}{\left(0,2\right)^6}=\dfrac{\left(0,2.3\right)^5}{\left(0,2\right)^5.\left(0,2\right)}=\dfrac{\left(0,2\right)^5.3^5}{\left(0,2\right)^5.\left(0,2\right)}=\dfrac{3^5}{0,2}=\dfrac{243}{0,2}=1215\)
c) \(2:\left(\dfrac{1}{2}-\dfrac{2}{3}\right)^2=2:\left(\dfrac{3}{6}-\dfrac{4}{6}\right)^2=2:\left(-\dfrac{1}{6}\right)^2=2:\dfrac{1}{36}=72\)

\(A=\dfrac{2^4.3^3+2^3.3^4}{2^5.3^4-2^6.3^3}=\dfrac{2^3.3^3.\left(2+3\right)}{2^5.3^3.\left(3-2\right)}=\dfrac{2^3.3^3.5}{2^5.3^3.1}\)
\(=\dfrac{5}{2^2}=\dfrac{5}{4}\)

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 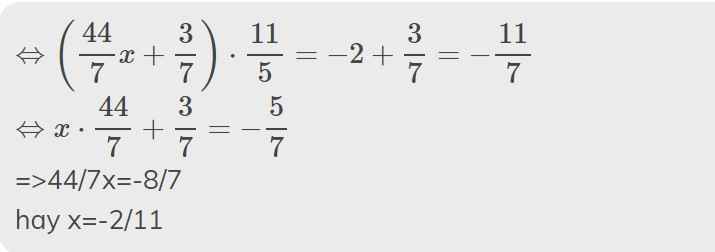
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

1. \(A=\dfrac{2\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}{4\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}=\dfrac{2}{4}=\dfrac{1}{2}\)
2. \(B=\dfrac{1^2.2^2.3^2.4^2}{1.2^2.3^2.4^2.5}=\dfrac{1}{5}\)
3.\(C=\dfrac{2^2.3^2.\text{4^2.5^2}.5^2}{1.2^2.3^2.4^2.5.6^2}=\dfrac{125}{36}\)
4.D=\(D=\left(\dfrac{4}{5}-\dfrac{1}{6}\right).\dfrac{4}{9}.\dfrac{1}{16}=\dfrac{19}{30}.\dfrac{1}{36}=\dfrac{19}{1080}\)
Lời giải:
Ta có: \(D=(2!)^2\left(\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+....+\frac{1}{2015^2}\right)\)
Xét số hạng tổng quát dạng \(\frac{1}{(2n+1)^2}\) với \(n\in\mathbb{N}\ge 1\)
Ta có: \((2n+1)^2-2n(2n+2)=1>0\)
\(\Rightarrow (2n+1)^2> 2n(2n+2)\Rightarrow \frac{1}{(2n+1)^2}< \frac{1}{2n(2n+2)}\)
Do đó: \(\left\{\begin{matrix} \frac{1}{3^2}< \frac{1}{2.4}\\ \frac{1}{5^2}< \frac{1}{4.6}\\ .....\\ \frac{1}{2015^2}< \frac{1}{2014.2016}\end{matrix}\right.\)
\(\Rightarrow \frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+...+\frac{1}{2015^2}< 1+\frac{1}{2.4}+\frac{1}{4.6}+....+\frac{1}{2014.1016}\)
\(\Leftrightarrow \frac{D}{(2!)^2}< 1+\frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+....+\frac{1}{2014.2016}\)
\(\Leftrightarrow D< 4\left(1+\frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+....+\frac{1}{2014.2016}\right)\)
\(\Leftrightarrow D< 4+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{1007.1008}\)
\(\Leftrightarrow D< 4+\frac{2-1}{1,2}+\frac{3-2}{2.3}+...+\frac{1008-1007}{1007.1008}\)
\(\Leftrightarrow D< 4+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{107}-\frac{1}{1008}\)
\(\Leftrightarrow D< 5-\frac{1}{1008}< 5< 6\)