A
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 11 2021
- Định nghĩa hai góc đối đỉnh : Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Định lí về hai góc đối đỉnh : Hai góc đối đỉnh thì bằng nhau.
- Định nghĩa hai đường thẳng vuông góc : Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90o
- Định nghĩa đường trung trực của một đoạn thẳng : Đường trung trực của đoạn thẳng là 1 đường thẳng vuông góc với đoạn thẳng và đi qua trung điểm của đoạn thẳng đó.
12 tháng 7 2019
- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Hai góc đối đỉnh thì bằng nhau.
- Hai đường thẳng xx′xx′ và yy′yy′ cắt nhau.Nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu xx′⊥yy′xx′⊥yy′.(Hình thì bạn tự vẽ nhé!)
- Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy.
5 tháng 9 2016
- Hai góc đối đỉnh là 2 góc mà 1 cạnh của góc này là tia đối của 1 cạnh của góc kia.
- Giả sử 2 đg thẳng xx' và yy' cắt nhau tại O mà trong các góc tạo thành có 1 góc = 90 độ
=> các góc còn lại = nhau và = 90 độ
LV
2
11 tháng 12 2019
Hai góc kề bù nằm kề nhau, có tổng = 180°.
Hai góc đối đỉnh có hai cạnh của hai góc đối với một trong hai cạnh của góc kia, tạo thành một hình dạng chữ X, bằng nhau.
11 tháng 12 2019
TL:
- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Ví dụ: Trong hình vẽ dưới đây thì ˆAOC A O C ^ và ˆBOD B O D ^ là hai góc đối đỉnh.
*Tính chất: Hai góc đối đỉnh thì bằng nhau.
17 tháng 9 2023
a)
b)
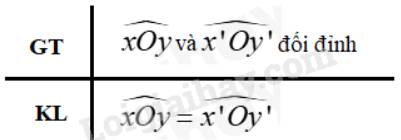
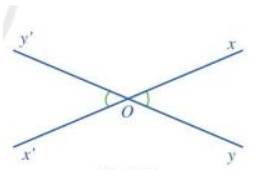
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
Hai góc đối đỉnh là hai góc mà mỗi cạnh là tia đối của một cạnh của góc kia
Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh.
tính chất Hai góc đối đỉnh thì bằng nhau.
Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Định lý : Hai góc đối đỉnh thì bằng nhau.
( Chú ý : Điều ngược lại của định lí chưa chắc đúng )