Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

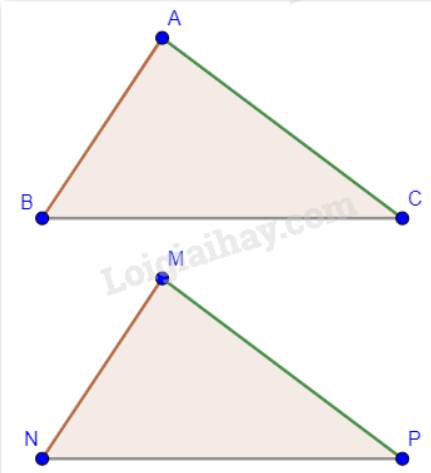
Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.

Do \(\Delta ABC = \Delta DEF\) nên \(\widehat B = \widehat E = {80^o}\); \(\widehat D = \widehat A = {60^o}\); \(\widehat C = \widehat F\) ( các góc tương ứng)
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 60^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 60^\circ - 80^\circ = 40^\circ \end{array}\)
Do đó \(\widehat F = 40^\circ \)
Vậy \(\widehat B = {80^o}; \widehat D ={60^o}; \widehat C = \widehat F= 40^\circ \).


Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).

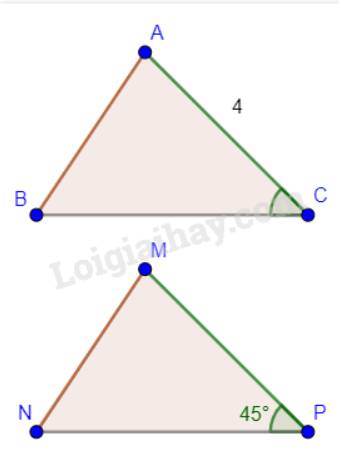
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).

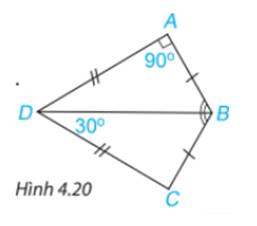
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)

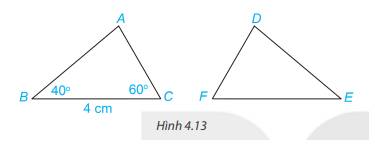
Vì \(\Delta ABC = \Delta DEF\) nên BC = EF ( 2 cạnh tương ứng); \(\widehat A = \widehat {EDF}\) ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 60^\circ = 180^\circ \\ \Rightarrow \widehat A = 180^\circ - 40^\circ - 60^\circ = 80^\circ \end{array}\)
Mà \(\widehat A = \widehat {EDF}\) nên \(\widehat {EDF} = 80^\circ \)

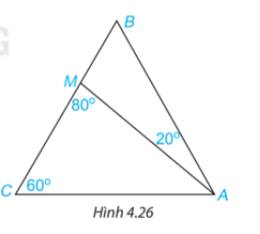
Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)

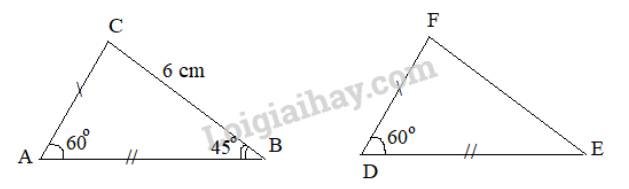
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

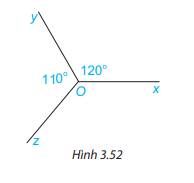
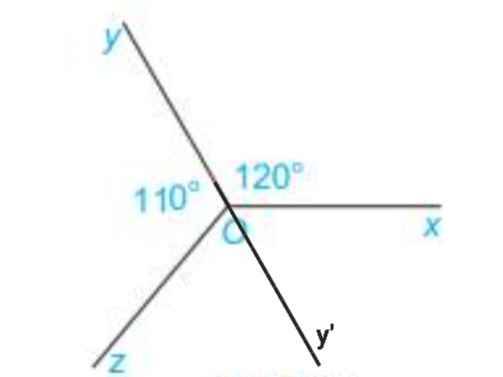 Vẽ tia Oy' là tia đối của tia Oy
Vẽ tia Oy' là tia đối của tia Oy
Ta có:
∠xOy + ∠xOy' = 180⁰ (kề bù)
⇒ ∠xOy' = 180⁰ - ∠xOy
= 180⁰ - 120⁰
= 60⁰
Lại có:
∠zOy + ∠zOy' = 180⁰ (kề bù)
⇒ ∠zOy' = 180⁰ - ∠zOy
= 180⁰ - 110⁰
= 70⁰
⇒ ∠zOx = ∠zOy' + ∠xOy'
= 70⁰ + 60⁰
= 130⁰
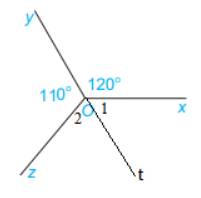
Kẻ Ot là tia đối của tia Oy.
Ta được:+) \(\widehat {{O_1}} + \widehat {xOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{O_1}} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {{O_1}} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
+) \(\widehat {{O_2}} + \widehat {yOz} = 180^\circ \)( 2 góc kề bù)
Vì Ot nằm giữa 2 tia Ox và Oz nên \(\widehat {xOz} = \widehat {{O_1}} + \widehat {{O_2}} = 60^\circ + 70^\circ = 130^\circ \)
Vậy \(\widehat {zOx} = 130^\circ \)
Ta có: \(\Delta PQR = \Delta IHK\)nên \(\widehat P = \widehat I;\widehat Q = \widehat H;\widehat R = \widehat K\).
\(\Rightarrow \widehat I = 71^\circ ,\widehat H = 49^\circ \). Mà tổng 3 góc trong một tam giác bằng 180° nên trong tam giác IHK:
\(\widehat I + \widehat H + \widehat K = 180^\circ \)
Vậy \(\widehat K = 180^\circ - 71^\circ - 49^\circ = 60^\circ \).