Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng dài nhất trong dãy Ban me khi nguyên tử chuyển từ mức 3 về 2 --> \(\dfrac{hc}{\lambda_{32}}=E_3-E_2=-\dfrac{13,6eV}{3^2}+\dfrac{13,6eV}{2^2}\) --> \(\lambda _{32}\)
Bước sóng ngắn nhất trong dãy pasen khi nguyên tử chuyển từ mức vô cùng về 3 --> \(\dfrac{hc}{\lambda}=E_n-E_3=0+\dfrac{13,6eV}{3^2}\)--> \(\lambda\)

\(E_n = -\frac{13,6}{n^2},(eV)\)(với n = 1, 2, 3,..)
Nguyên tử hiđrô hấp thụ một phôtôn có năng lượng 2,55 eV.
Việc đầu tiên là cần phải xác định xem nguyên tử nhảy từ mức nào lên mức nào mà có hiệu năng lượng giữa hai mức đúng bằng 2,55 eV.
\(E_1 = -13,6eV\), \(E_3 = -1,51 eV\)
\(E_2 = -3,4eV\),\(E_4 = -0,85eV\)
Nhận thấy \(E_4-E_2= -0,85 +3,4= 2,55 eV.\)
Như vậy nguyên tử đã hấp thụ năng lượng và nhảy từ mức n = 2 lên mức n = 4.
Tiếp theo, nguyên tử đang ở mức n = 4 rồi thì nó có thể phát ra bước sóng nhỏ nhất ứng với từ n = 4 về n = 1 tức là \(\lambda_{41}\) thỏa mãn
\(\lambda_{41}= \frac{hc}{E_4-E_1}= \frac{6,625.10^{-34}.3.10^8}{(-0,85+13,6).1,6.10^{-19}}=9,74.10^{-8}m. \)

Đáp án D
Công thức tính số bức xạ tối đa mà nguyên tử có thể phát ra
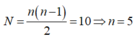
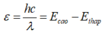
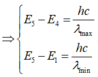
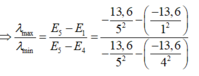
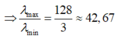

Khi electron nhảy từ trạng thái có năng lượng En sang trạng thái có mức năng lượng nhỏ hơn Em thì nguyên tử phát ra bức xạ thỏa mãn
\(hf = E_n-E_m \)
=> \(h\frac{c}{\lambda} = E_m-E_n \)
=> \(\lambda=\frac{hc}{E_m-E_n} =\frac{6,625.10^{-34}.3.10^8}{1,9.1,6.10^{-19}}=6,54.10^{-7}m= 0,654.10^{-6}m.\)

+ Vận tốc của electron khi nó chuyển động trên quỹ đạo thứ n: v ~ 1 n
→ Động năng giảm 9 lần → v giảm 3 lần → n = 6.
+ Bước sóng dài nhất ứng với sự chuyển mức năng lượng từ E6 về E5, bước sóng nhìn thấy ngắn nhất ứng với sự chuyển mức năng lượng từ E6 về E2.
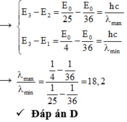




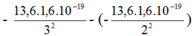
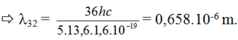
Xét trong dãy thứ n, ta có:
+ Bước sóng lớn nhất khi nguyên tử chuyển từ mức n + 1 về n, do vậy ta có:
\(\dfrac{hc}{\lambda_{max}}=E_{n+1}-E_{n}\) (1)
+ Bước sóng nhỏ nhất khi nguyên tử chuyển từ mức \(\infty\) (có năng lượng = 0) về mức n, ta có:
\(\dfrac{hc}{\lambda_{min}}=0-E_{n}\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\lambda_{max}}{\lambda_{min}}=\dfrac{-E_n}{E_{n+1}-E_n}=\dfrac{\dfrac{1}{n^2}}{\dfrac{1}{n^2}-\dfrac{1}{(n+1)^2}}\)
\(\Rightarrow \dfrac{\lambda_{max}}{\lambda_{min}}=\dfrac{(n+1)^2}{(n+1)^2-n^2}==\dfrac{(n+1)^2}{2n+1}\)
Chọn đáp án B.