Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a( ax + 1) = x(a + 2) + 2
<=>a2x+a=xa+2x+2
<=>a2x-xa-2x=2-a
<=>x.(a2-a-2)=2-a
<=>x=\(\frac{2-a}{a^2-a-2}=\frac{-\left(a-2\right)}{a^2-2a+a-2}=\frac{-\left(a-2\right)}{a.\left(a-2\right)+\left(a-2\right)}=\frac{-\left(a-2\right)}{\left(a-2\right)\left(a+1\right)}=\frac{-1}{a+1}\)

a)x(x+3)+a(x-3)=2(ax-1)
=>x2+3x+ax-3a=2ax-2
=>x2+3x+ax-3a-2ax=-2
=>x2+3x-ax-3a = -2
=> (x2+3x)-(ax+3a)=-2
=>x(x+3)-a(x+3)=-2
=>(x+3)(x-a)=-2
=>x+3và x-a\(\in\)U(-2)
| x+3=>x | x-a=>a | |
| -2 | x=-5 |
a=-6 |
| -1 | x=-4 | a=-6 |
| 1 | x=-2 | a=0 |
| -2 | x=-1 | a=-3 |
vậy S={-5;-4;-2;-1}lần lượt tương ứng với a\(\in\){-6(hai lân);0;-3}


ĐKXĐ: x\(\ne3,x\ne-3\)
\(\Rightarrow\left(x-a\right)\left(a-3\right)+\left(x+3\right)\left(a+3\right)=-6a\)
\(\Leftrightarrow xa-3x-a^2+3a+ax+3x+3a+3=-6a\)
\(\Leftrightarrow2ax-a^2+12a+3=0\) \(\Leftrightarrow2ax=a^2-12a-3\Leftrightarrow x=\dfrac{a^2}{2}-6a-\dfrac{3}{2}\)(TM)
Vậy...

\(\Leftrightarrow\dfrac{x}{a}-x>4-a-\dfrac{3}{a}\)
\(\Leftrightarrow x\left(\dfrac{1}{a}-1\right)>\dfrac{4a-a^2-3}{a}\)
- Nếu \(\dfrac{1}{a}-1>0\Leftrightarrow0< a< 1\)
\(\Rightarrow x>\dfrac{4a-a^2-3}{a\left(\dfrac{1}{a}-1\right)}\Leftrightarrow x>a-3\)
- Nếu \(\dfrac{1}{a}-1< 0\Leftrightarrow\left[{}\begin{matrix}a< 0\\a>1\end{matrix}\right.\)
\(\Rightarrow x< \dfrac{4a-a^2-3}{a\left(\dfrac{1}{a}-a\right)}\Leftrightarrow x< a-3\)

\(\frac{ax-b}{a}+(a+b+1)x>\frac{2b}{a}\)
<=> \(x-\frac{b}{a}+\left(a+b+1\right)x>\frac{2b}{a}\)
<=> \(\left(a+b+2\right)x>\frac{3b}{a}\)
Giờ biện luận theo a và b thôi

Điều kiện xác định: a ≠ 0.
Ta có: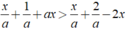
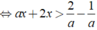
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là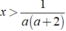
+ Nếu a < - 2 thì nghiệm của bất phương trình là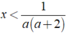
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
x=-1 với a=1.