Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi r và h lần lượt là bán kính đáy và độ dài đường cao hình nón
Thể tích hình nón : 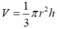
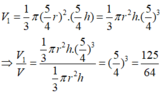
Vậy chọn đáp án D

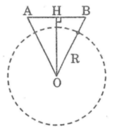
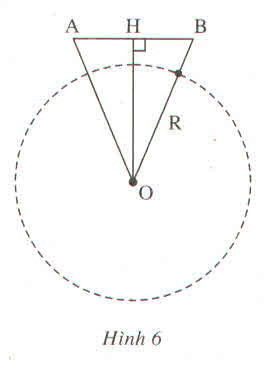
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
Suy ra: HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
O A 2 = A H 2 + O H 2
Suy ra: O H 2 = O A 2 - A H 2
Suy ra:
OH = ![]() ≈ 6508 (km)
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.

Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
\(\Rightarrow\): HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
OA2 = AH2 + OH2
\(\Rightarrow\): OH2 = OA2 – AH2
\(\Rightarrow\) :OH = 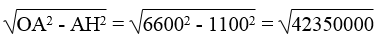
Vì OH > R nên hai vệ tinh nhìn thấy nhau.



Chọn (D)