Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Kí hiệu \(S\) là tổng tất cả các số trên cùng 1 hàng, cột hay đường chéo. Dễ dàng kiểm chứng được \(-6\le S\le6\). Ta thấy từ \(-6\) đến \(6\) có tất cả là 13 số nguyên. Nói cách khác, sẽ có tất cả 13 giá trị khác nhau mà \(S\) có thể đạt được. Do trên bảng 6x6 có 6 cột, 6 hàng, 2 đường chéo ứng với 14 tổng S nên theo nguyên lí Dirichlet, sẽ tồn tại 2 tổng S mang cùng 1 giá trị, đây là đpcm.
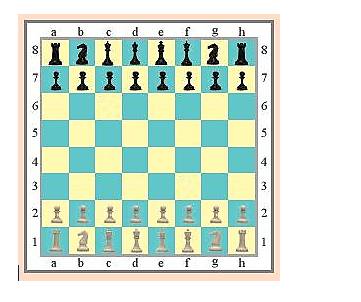
Quan sát bàn cờ ta thấy
- Quân Hậu Trắng đang ở giao của hàng 1 và cột d.
- Tại giao của cột b và hàng 8 là quân Mã đen.
Cho bàn cờ 5 *5 dùng các số tự nhiên từ 1 - 25 điền vào bàn cờ sao cho tổng các số ở hàng ngang, cột dọc , đường chéo bằng nhau. Chứng tỏ rằng với các bàn cờ a*a với a lẻ ta luôn có quy luật điền giống nhau. Bạn dùng ma phương thử đi.
Cho bàn cờ 5 *5 dùng các số tự nhiên từ 1 - 25 điền vào bàn cờ sao cho tổng các số ở hàng ngang, cột dọc , đường chéo bằng nhau. Chứng tỏ rằng với các bàn cờ a*a với a lẻ ta luôn có quy luật điền giống nhau. Bạn dùng ma phương thử xem.
Cho bàn cờ 5 *5 dùng các số tự nhiên từ 1 - 25 điền vào bàn cờ sao cho tổng các số ở hàng ngang, cột dọc , đường chéo bằng nhau. Chứng tỏ rằng với các bàn cờ a*a với a lẻ ta luôn có quy luật điền giống nhau. Bạn dùng ma phương thử xem.
| a | b | c | d | e | |
| 5 | |||||
| 4 | |||||
| 3 | |||||
| 2 | |||||
| 1 |
Ta đánh dấu bảng 5x5 như trên và không mất tính tổng quát, giả sử quân mã ban đầu ở vị trí a1. Khi đó một đường đi của quân mã để đi hết tất cả các ô trên bàn cờ (với điều kiện mỗi ô chỉ được đi qua 1 lần) là:
a1-c2-e1-d3-e5-c4-a5-b3-c1-e2-d4-b5-a3-b1-d2-e4-c5-a4-b2-d1-e3-d5-b4-a2-c3.
cái này đúng rồi á chị nhưng mà nhìn bàn cờ nó cũng cứ kiểu gì ấy....
Hì hì...