Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

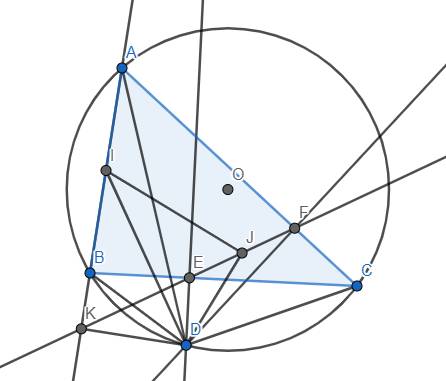
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm


Bạn A,B,C,D,E,F,G có dự định đi mua vở ghi mà bạn F và G có dự định mua thêm 2 cái bút hết 3k hai cái. Mua vở thì
bạn D góp 20k, bạn A góp 6k , bạn G góp 51k và bạn F góp 22k thì tổng là 77k tất cả nhưng bạn B,C,E chưa góp. Bạn F,G nhận đi mua và giao vở lấy ship 1k/ bạn. Sau khi đi mua vở , bút xong hết 93k tất cả ( trong đó có 6 bạn A,B,C,D,E và G mua 6 quyển vở giá 15k trên 1 quyển , F và G mua bút như dự định trên ) . Sau khi mua xong bạn B,C,E trả đủ 16k , bạn D thừa 4k , bạn A thiếu 10k. Hỏi tổng số tiền của bạn F và G sau khi đi giao vở thì còn lại bao nhiêu ? ( trừ tiền mua bút như dự định và cộng 6k tiền lãi ship chia đôi cho 2 bạn ) biết rằng sau khi đi giao vở cho mỗi bạn thì F và G lãi 1k/ bạn tiền ship. TÍNH RÕ TIỀN SAU TẤT CẢ CỦA F VÀ G.

Vì BE vuông góc với AC tại E (E ϵAC) ⇒ góc BEC =\(90^0\)
Vì CF vuông góc với AB tại F (F ϵ AB) ⇒ góc BFC =\(90^0\)
xét tứ giác BCEF có ;
góc BEC+BFC=\(90^0+90^0=180^0\)
mà hai góc ở vị trí kề nhau
⇒tứ giác BCEF là tgnt hay A,C,E,F cùng nằm trên một đtròn
b,

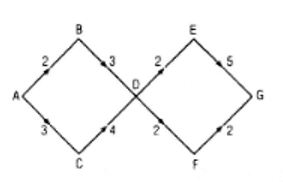
Có 4 phương án đi qua các tỉnh A đến G là:
a) A → B → D → E → G
b) A → B → D → F → G
c) A → C → D → E → G
d) A → C → D → F → G
Theo quy tắc nhân ta có:
Phương án a) có 2.3.2.5 = 60 cách đi
Phương án b) có 2.3.2.2 = 24 cách đi
Phương án c) có 3.4.2.5 = 120 cách đi
Phương án d) có 3.4.2.2 = 48 cách đi
Vậy theo quy tắc cộng có 60 + 24 + 120 + 48 = 252 cách đi từ A đến G.
Có 4 phương án đi qua các tỉnh A đến G là :
a. A → B → D → E → G
b. A → B → D → F → G
c. A → C → D → E → G
d. A → C → D → F → G
Theo quy tắc nhân, ta có :
Phương án a có 2.3.2.5=60 cách đi;
Phương án b có 2.3.2.2=24 cách đi;
Phương án c có 3.4.2.5=120 cách đi;
Phương án d có 3.4.2.2=48 cách đi.
Theo quy tắc cộng, ta có : 60+24+120+48=252 cách đi từ A đến G.