Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

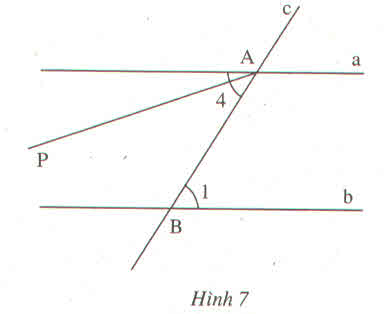
Ta có : ˆA1A1^ và ˆA2A2^ là hai góc kề bù nên:
ˆA1+ˆA2=1800⇒ˆA2=1800−ˆA1=1800−1500=300A1^+A2^=1800⇒A2^=1800−A1^=1800−1500=300
Vì d1 // d2 và ˆA2A2^ so le trong với ˆB1B1^
⇒ˆB1=ˆA2=300⇒B1^=A2^=300
Vậy ˆB1=300
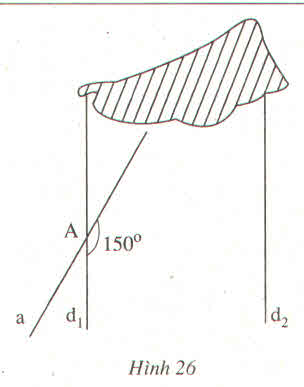
Gọi B giao điểm của a và d2.
d1 // d2 nên góc nhọn tại B bằng góc nhọn tại A và bằng
1800 - 1500= 300.

Hướng dẫn:
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 1800 (2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 12121800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ +

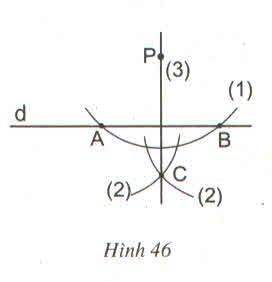
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
Hướng dẫn:
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)

a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:
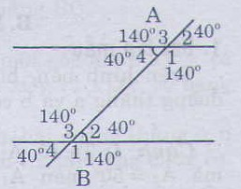
c) Ta có:
góc A4 + A1 = 180độ
=> góc A1 = 180 độ - 40 độ = 140 độ
=> góc A1 + góc B2= 40độ + 140 độ = 180 độ
Ý 2
Ta có:
góc B3 + góc B2 = 180 độ
=> góc B3 = 180 độ - 40 độ = 140 độ
=> góc A4 + B3 = 140 độ + 40 độ = 180 độ


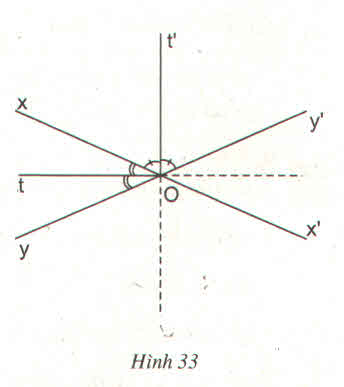



a) Ba đường thẳng cắt nhau tại O tạo thành 6 tia. Số góc do 6 tia tạo ra là: 6.5 2 = 15 (góc).
b) Xét hai đường thẳng AB và CD trong ba đường thẳng đã cho (h.1.11). Hai đường thẳng này tạo thành bốn góc không có điểm trong chung. Tổng của bốn góc này bằng 360 ° nên trong bốn góc đó phải tồn tại một góc lớn hơn hoặc bằng 90 ° .
Thật vậy, nếu mỗi góc đó đều nhỏ hơn 90 ° thì tổng của chúng nhỏ hơn 90 ° .4 = 360 ° : vô lí.
Giả sử góc tồn tại nói trên là góc BOD.
- Nếu B O D ^ > 90 ° thì A O C ^ = B O D ^ > 90 ° , bài toán đã giải xong.
- Nếu B O D ^ = 90 ° thì ta xét tiếp đường thẳng thứ ba MN đi qua O (h.1.12).
Giả sử tia ON nằm trong góc BOD. Khi đó góc BON là góc nhọn do đó A O N ^ là góc tù (vì B O N ^ và A O N ^ là hai góc kề bù). Góc AON là góc tù thì góc BOM là góc tù (vì B O M ^ = A O N ^ ).
Vậy luôn tồn tại hai góc tù trong số 15 góc được tạo thành.
Chứng tỏ hai tia đối nhau