Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vì BN=AC mà AC=AM'
=> BN=AM' (tính chất bắc cầu)
vì BN=AM', AB=AB
=>AN=BM'
Vì BN'=BC mà BC=AM
=>BN'=AM
Vì BN'=AM, AB=AB
=>AN'=BM
Vì BN=AC ,AM=BC
=>MC=NC
b) mình chịu

a) +) Xét \(\Delta\)AM'B và \(\Delta\)BNA có;
^M'AB = ^NBA = 90o
AB chung
AM' = BN ( = AC)
=> \(\Delta\)AM'B = \(\Delta\)BNA
=> AN = BM'
+) Vì AM' = ABN ; AM = BN' ( = BC )
=> AM = BN'
^MAB = ^N'BA = 90o
=> \(\Delta\)AMB = \(\Delta\)BN'A
=> AN' = BM
+) Xét \(\Delta\)AMC và \(\Delta\)BCN có:
AM = BC
BN = AC
^MAC = ^CBN ( = 90o )
=> \(\Delta\)AMC = \(\Delta\)BCN
=> MC = NC
b) \(\Delta\)AM'B = \(\Delta\)BNA ( chứng minh ở a)
=> ^M'BA = ^NAB mà hai góc này ở vị trí so le trong
=> AN // BM'
\(\Delta\)AMB = \(\Delta\)BN'A
=> ^MBA = ^N'AB mà hai góc này ở vị trí so le trong
=> MB // AN'
c) Gọi O là trung điểm của AB
Xét \(\Delta\)OAM và \(\Delta\)OBN' có:
OA = OB
^OAM = ^OBN'
AM = BN'
=> \(\Delta\)OAM = \(\Delta\)OBN' => ^AOM = ^BON' mà ^AOM + ^MOB = 180o => ^BON' + ^MOB = 180o => MON' = 180o
=> M; O; N' thẳng hàng (1)
Tương tự chứng minh được:
\(\Delta\)OAM' = \(\Delta\)OBN
=> M'; O; N thẳng hàng (2)
Từ (1); (2) => MN' và M'N cắt nhau tại điểm O là trung điểm của AB


a) Giả sử ta kẻ My \(\perp\)BC cắt Bx tại A'
Kết hợp với ^CBx = 450 suy ra \(\Delta\)A'MB vuông cân tại M
=> \(\frac{BM}{BA'}=\frac{1}{\sqrt{2}}\)Lại có \(\frac{BM}{BA}=\frac{1}{\sqrt{2}}\)nên \(BA'\equiv BA\)
\(\Rightarrow A'\equiv A\)nên AM \(\perp\)BC
Kết hợp với CI \(\perp\)AD suy ra N là trực tâm của \(\Delta\)ADC
Suy ra DN \(\perp\)AC (đpcm)
b) Xét \(\Delta\)AMB và \(\Delta\)AMC có:
MB = MC (gt)
^AMB = ^AMC ( = 900)
AM : cạnh chung
Do đó \(\Delta\)AMB = \(\Delta\)AMC (c.g.c)
=> AB = AC (hai cạnh tương ứng) và ^MBA = ^MCA (=450) => ^BAC = 900
Xét \(\Delta\)AIC (^AIC = 900) và \(\Delta\)AHB (^AHB = 900) có:
AB = AC (cmt)
^ABH = ^ACI (cùng phụ với ^BAH)
Do đó \(\Delta\)CIA = \(\Delta\)AHB (ch-gn)
=> AI = BH
=> BH2 + CI2 = AI2 +CI2 =AC2 (không đổi)
c) Xét \(\Delta\)BHM và \(\Delta\)AIM có:
AI = BH (cmt)
^HBM = ^IAM (cùng phụ với hai cặp góc đối đỉnh là ^BDH và ^ADM)
BM = AM (cmt)
Do đó \(\Delta\)BHM = \(\Delta\)AIM
=> HM = IM (1) và ^HMB = ^IMA
Mà ^IMA + ^IMD = 900 nên ^HMB + ^IMD = 900 (2)
Từ (1) và (2) suy ra \(\Delta\)HMI vuông cân tại M => ^HIM = 450
Lại có ^HIC = 900 nên IM là phân giác của ^HIC
Vậy tia phân giác của góc HIC luôn đi qua một điểm cố định M (đpcm)

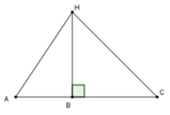
Vì BH là đường vuông góc và AH là đường xiên nên AH > BH
Chọn đáp án C.

a,Vì :
\(AM\mp BC,CI\)\(\Omega\)\(AD,CI\)\(\Omega\)\(AM=N\)
\(\rightarrow N\)là trực tâm \(\Delta ADC\rightarrow DN\)\(\Omega\)\(AC\)
b,Vì :
\(\widehat{BAC}=45^O,\frac{BM}{BA}=\frac{1}{\sqrt{2}}\rightarrow\Delta ABM\) vuông cân tại \(M\)
\(\rightarrow\Delta ABC\) vuông cân tại \(A\)
\(\rightarrow AB=AC\)MÀ
\(\widehat{BAH}=\widehat{ACI}\left(+\widehat{DAC}=90^O\right),\widehat{AHB}\)
\(=\widehat{AIC}=90^O\)
\(\rightarrow\Delta ABH=\Delta CAI\left(g,c,g\right)\)
\(\rightarrow BH=AI\rightarrow BH^2+CI^2=AI^2+CI^2=AC^2=AB^2=2BM^2=\frac{BC^2}{2}=const\)
c,Ta có
\(\widehat{AIC}=\widehat{NMC}=90^O\rightarrow\widehat{IAN}=\widehat{NCM}\)
\(\rightarrow\Delta AIN~\Delta CMN\left(g.g\right)\rightarrow\frac{AN}{CN}=\frac{IN}{MN}\)
\(\rightarrow\Delta NIM~\Delta NAC\left(c.g.c\right)\rightarrow\widehat{MIN}=\widehat{NAC}=45^O\)Mà:
\(CI\) ! \(ID\rightarrow IM\)Là phân giác \(\widehat{CIH}\)\(\rightarrow\)Tia phân giác của góc HIC luôn đi qua 1 điểm M cố định.
Lưu ý : \(\mp\)Thay cho !
\(\Omega\)thay cho
NHiều công thức mk ko thấy nên là mk viết thay bằng cái khác tương tự xíu nha bn

Bài 3:
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AD=BC
b: Ta có: ABCD là hình bình hành
nên CD//AB
mà AB⊥AC
nên CD⊥AC
c: Xét tứ giác ABNC có
AB//NC
BN//AC
Do đó: ABNC là hình bình hành
Suy ra: AB=CN
Xét ΔBAM vuông tại A và ΔNCM vuông tại C có
MA=MC
BA=NC
Do đó: ΔBAM=ΔNCM

Câu hỏi của kakemuiki - Toán lớp 7 - Học toán với OnlineMath
Chọn B