Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
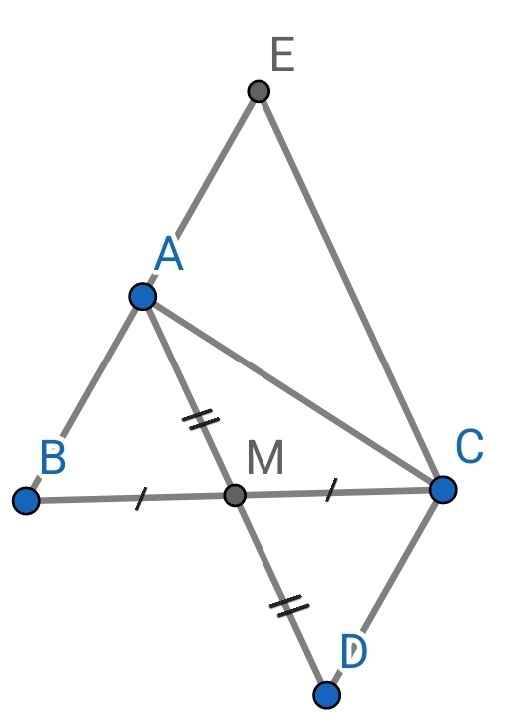a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE
b) Vì AC=2AB
AB=BD
=>AC=AD
Xét tam giác ACE và tam giác ADE có:
AC=AD ( chứng minh trên )
^CAE=^EAD ( tính chất phân giác )
AE chung
=> tam giác ACE = tam giác ADE ( c.g.c )
=> ^CEA=^AED ( 2 góc tương ứng )
Mà ^CEA kề bù ^AED
=> ^CEA=^AED=90°
=> AE vuông góc CD
AI và AE là 2 tia trùng nhau
=> AI vuông góc CD
Vì AI vuông góc BM
Mà AI vuông góc CD
<=> BM // CD
Chúc bạn học tốt!
Vì mình không tìm được cách gõ góc nên kí hiệu ^ là góc nhé! Mong bạn thông cảm
a. Xét tam giac ABM và tam giac ACM có
AB=AC(gt)
góc B=góc C(tam giac ABC cân)
AM cạnh chung
suy ra tam giac ABM=tam giac ACM
b. ta có:
tam giác ABC cân mà AM là đường trung tuyến nên AM cũng là đường cao
suy ra AM vuông goc vs BC
Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá
3/ (Bạn tự vẽ hình giùm)
a/ \(\Delta ABC\)và \(\Delta ADC\)có:
\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)
Cạnh AC chung
\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)
=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)
=> AD = BC (hai cạnh tương ứng)
và AB = DC (hai cạnh tương ứng)
b/ Ta có AD = BC (cm câu a)
và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)
và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)
=> AN = MC
Chứng minh tương tự, ta cũng có: BM = ND
\(\Delta AMB\)và \(\Delta CND\)có:
BM = ND (cmt)
\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)
AB = CD (\(\Delta ABC\)= \(\Delta ADC\))
=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)
=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)
và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))
=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)
=> \(\widehat{MAC}=\widehat{ACN}\)(1)
Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)
và AN = MC (cmt) (3)
=> \(\Delta MAC=\Delta NAC\)(g, c. g)
=> AM = CN (hai cạnh tương ứng) (đpcm)
c/ \(\Delta AOB\)và \(\Delta COD\)có:
\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)
AB = CD (cm câu a)
\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)
=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)
=> OA = OC (hai cạnh tương ứng)
và OB = OD (hai cạnh tương ứng)
d/ \(\Delta ONA\)và \(\Delta MOC\)có:
\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)
OA = OC (O là trung điểm AC)
\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)
=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)
=> ON = OM (hai cạnh tương ứng)
=> O là trung điểm MN
=> M, O, N thẳng hàng (đpcm)
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD