Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ABCD là HBH nên:
*OB=OD từ đó BM=OM=ON=BN => ON=OM (1)
*OA=OC (2)
Từ 1,2 => AMCN là HBH ( 2 đường chéo cắt nhau tại trung điểm mỗi đường)^^
b) Để AMCN là hình thoi, phải có AC vuông góc với MN
Suy ra tứ giác ABCD phải là hình thoi (2 đường chéo vuông góc)^^
vẽ CH vuông góc BN,CK vuông góc DM
Tam giác COK=Tam giác COH(ch-gn)
=> CK=CH
S_NBC=CH.BN/2,S_MDC=CK.DM/2,S_NBC=S_MDC(=S_DBC)
=>BN=DM

a)Ta có O giao điểm AC và BD trong hình bình hành ABCD (gt)
=> O là trung điểm AC và BD.
=> OD=OB
Mà OM=MD=\(\frac{1}{2}\)OD; ON=BN=\(\frac{1}{2}\)OB => OM=ON=OD=OB.
Xét hình bình hành ABCD có O trung điểm AC (hbh ABCD) và O trung điểm MN (OM=ON)
=> đpcm (điều phải chứng minh)
b) C/m tam giác ACE=ACF (cgc)(AC chung; \(\angle EAC=\angle FCA\) do song song; và cũng như vây với \(\angle ECA=\angle CAF\))
=>AE=FC mà \(AE \parallel FC\) do ăn theo hbh AMCN => đpcm

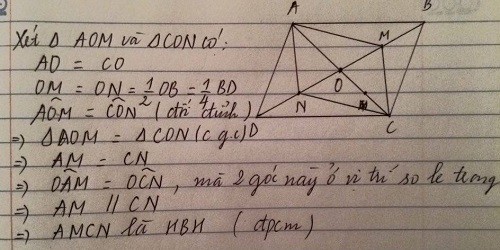
giúp mik ik