Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMKN có
\(\widehat{AMK}=\widehat{ANK}=\widehat{NAM}=90^0\)
Do đó: AMKN là hình chữ nhật

Lời giải:
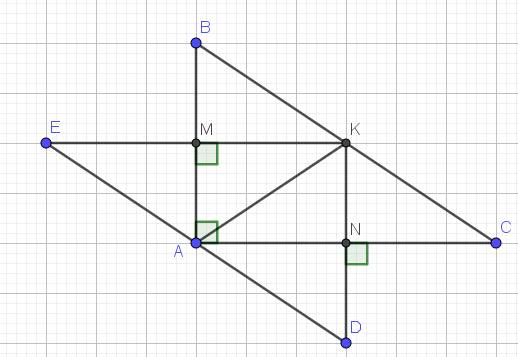
a. Tứ giác $AMKN$ có 3 góc vuông $\widehat{A}=\widehat{M}=\widehat{N}=90^0$ nên $AMKN$ là hình chữ nhật.
b.
Xét tam giác $AEM$ và $AKM$ có:
$MA$ chung
$\widehat{AME}=\widehat{AMK}=90^0$
$EM=KM$ (do $E,K$ đối xứng nhau qua $M$)
$\Rightarrow \triangle AEM=\triangle AKM$ (c.g.c)
$\Rightarrow \widehat{EAM}=\widehat{KAM}(1)$
Tương tự:
$\triangle AKN=\triangle ADN$ (c.g.c)
$\Rightarrow \widehat{DAN}=\widehat{KAN}(2)$
Từ $(1); (2)\Rightarrow \widehat{EAM}+\widehat{MAN}+\widehat{DAN}=\widehat{KAM}+\widehat{MAN}+\widehat{KAN}=2\widehat{MAN}=2.90^0=180^0$
Hay $\widehat{EAD}=180^0$
$\Rightarrow E, A, D$ thẳng hàng.

B C A M H K N D O I
a) Xét tứ giác BHMK có 3 góc vuông nên nó là hình chữ nhật.
Khi đó hai đường chéo bằng nhau nên BM = HK.
b) Xét tam giác ABC có M là trung điểm AC, MK // AB nên MK là đường trung bình.
Vậy thì K là trung điểm BC.
Xét tứ giác BMCN có K là trung điểm hai đường chéo nên nó là hình bình hành.
Lại có MN vuông góc BC nên BMCN là hình thoi.
Dễ thấy rằng MK = AB/2 hay MN = AB.
Để hình thoi BMCN là hình vuông thì MN = BC hau AB = BC.
Vậy tam giác ABC là tam giác vuông cân tại B thì BMCN là hình vuông.
c) Ta có BHMK là hình chữ nhật nên BM giao HK tại trung điểm mỗi đường.
Dễ thấy tứ giác ABNM có AB song song và bằng NM nên nó là hình bình hành.
Vậy nên BM giao AM tại trung điểm mỗi đoạn.
Từ đó ta có BM, HK, AN đồng quy tại trung điểm mỗi đoạn.
d) Gọi giao điểm của BM, HK và AN làO, giao của BM và AK là I.
Ta có: do KM // AB, áp dụng Talet:
\(\frac{IM}{BI}=\frac{MK}{AB}=\frac{1}{2}\Rightarrow\frac{IM}{BO+OI}=\frac{1}{2}\Rightarrow\frac{IM}{IM+OI+OI}=\frac{1}{2}\)
\(\Rightarrow IM=2OM\)
Áp dụng Talet cho tam giác AND và ADC ta có:
\(\frac{OI}{DN}=\frac{AI}{AD}=\frac{IM}{DC}\Rightarrow\frac{OI}{DN}=\frac{IM}{DC}\Rightarrow DC=2ND\)
a) Xét tứ giác ANMK có:
\(\left\{{}\begin{matrix}\widehat{A}=90^o\\\widehat{N}=90^o\\\widehat{K}=90^o\end{matrix}\right.\)
=> ANMK là hình chữ nhật
b) Ta có:
\(\widehat{MCA}=\widehat{MAC}=\widehat{NAK}\) mà 2 góc có vị trí đồng vị
=> NK//MC
Mặt khác: MN//KC
=> NMCK là hình bình hành
Ta có: O là trung điểm MK
=> O là trung điểm NC
=> ON=OC
c)
Vì tứ giác ANMK là hình chữ nhật
=> NM=AK
tứ giác NMCK là hình bình hành
=> NM=KC
=> \(MN=\dfrac{1}{2}AC\)
\(\Rightarrow EM=AC\)
mà EM//AC
=> AEMC là hình bình hành
Gọi I là trung điểm AM
=> I là trung điểm EC
Vì ANMK là h.c.n
=> I là trung điểm NK
=> AM, NK, EC đồng quy tại I