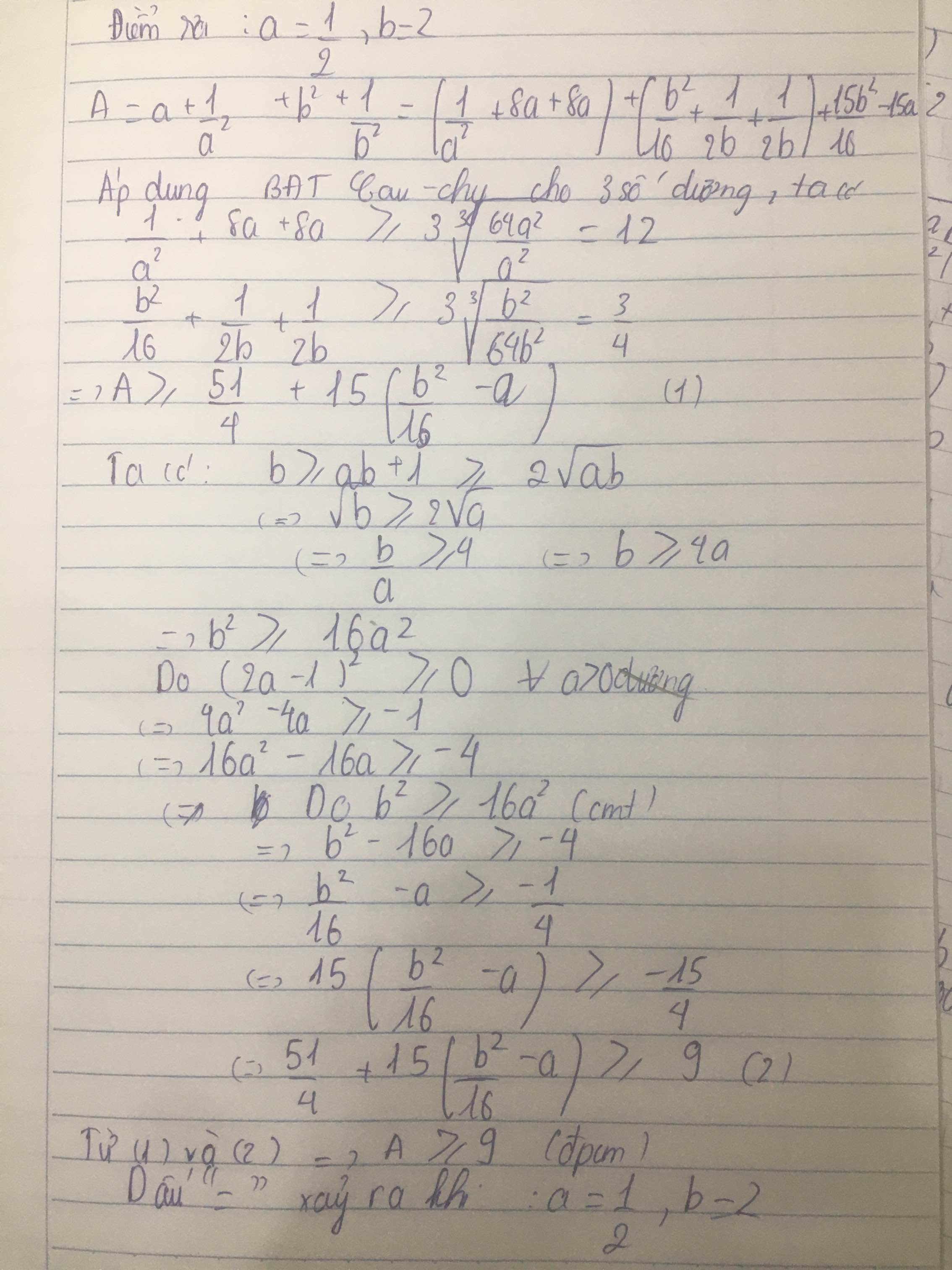Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng BĐT Cauchy Schwarz dạng engel , ta có :
\(VP=\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\ge\frac{3^2}{3+3}=\frac{3}{2}\)
Dấu = xảy ra khi và chỉ khi \(x=y=z=1\)
Vậy \(T\)đạt giá trị nhỏ nhất là \(\frac{3}{2}\)với x = y = z = 1
đặt \(\sqrt{\frac{ab}{c}}=x;\sqrt{\frac{bc}{a}}=y;\sqrt{\frac{ca}{b}}=z\Rightarrow xy+yz+zx=1\)
\(P=\frac{ab}{ab+c}+\frac{bc}{bc+a}+\frac{ca}{ca+b}\)
\(=\frac{\frac{ab}{c}}{\frac{ab}{c}+1}+\frac{\frac{bc}{a}}{\frac{bc}{a}+1}+\frac{\frac{ca}{b}}{\frac{ca}{b}+1}=\frac{x^2}{x^2+1}+\frac{y^2}{y^2+1}+\frac{z^2}{z^2+1}\)
\(\ge\frac{\left(x+y+z\right)^2}{\left(x+y+z\right)^2+\frac{\left(x+y+z\right)^2}{3}}=\frac{3}{4}\left(Q.E.D\right)\)
C6. Cho các số thực dương thoả mãn: ab+1 nhỏ hơn hoặc bằng b Chứng minh rằng : ( a + (1/a^2) ) + ( b^2 + (1/b) ) lớn hơn hoặc bằng 9
\(ab+1\le b\Rightarrow a+\dfrac{1}{b}\le1\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x+y\le1\)
Gọi vế trái của BĐT cần chứng minh là P:
\(P=x+\dfrac{1}{x^2}+y+\dfrac{1}{y^2}=\left(\dfrac{1}{x^2}+8x+8x\right)+\left(\dfrac{1}{y^2}+8y+8y\right)-15\left(x+y\right)\)
\(P\ge3\sqrt[3]{\dfrac{64x^2}{x^2}}+3\sqrt[3]{\dfrac{64y^2}{y^2}}-15.1=9\) (đpcm)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) hay \(\left(a;b\right)=\left(\dfrac{1}{2};2\right)\)
\(\sqrt{a^2+\dfrac{1}{b+c}}=\dfrac{2}{\sqrt{17}}\sqrt{\left(4+\dfrac{1}{4}\right)\left(a^2+\dfrac{1}{b+c}\right)}\ge\dfrac{2}{\sqrt{17}}\left(2a+\dfrac{1}{2\sqrt{b+c}}\right)\)
\(\Rightarrow A\ge\dfrac{1}{\sqrt{17}}\left(4a+4b+4c+\dfrac{1}{\sqrt{a+b}}+\dfrac{1}{\sqrt{b+c}}+\dfrac{1}{\sqrt{c+a}}\right)\)
\(\Rightarrow A\ge\dfrac{1}{\sqrt{17}}\left(4a+4b+4c+\dfrac{9}{\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}}\right)\)
Mặt khác:
\(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\le\sqrt{3\left(a+b+b+c+c+a\right)}=\sqrt{6\left(a+b+c\right)}\)
\(\Rightarrow A\ge\dfrac{1}{\sqrt{17}}\left(4a+4b+4c+\dfrac{9}{\sqrt{6\left(a+b+c\right)}}\right)\)
\(\Rightarrow A\ge\dfrac{1}{\sqrt{17}}\left(\dfrac{31}{8}\left(a+b+c\right)+\dfrac{a+b+c}{8}+\dfrac{9}{2\sqrt{6\left(a+b+c\right)}}+\dfrac{9}{2\sqrt{6\left(a+b+c\right)}}\right)\)
\(\Rightarrow A\ge\dfrac{1}{\sqrt{17}}\left(\dfrac{31}{8}.6+3\sqrt[3]{\dfrac{81\left(a+b+c\right)}{32.6.\left(a+b+c\right)}}\right)=\dfrac{3\sqrt{17}}{2}\)
Dấu "=" xảy ra khi \(a=b=c=2\)
a2(b+c)2+5bc+b2(a+c)2+5ac≥4a29(b+c)2+4b29(a+c)2=49(a2(1−a)2+b2(1−b)2)(vì a+b+c=1)
a2(1−a)2−9a−24=(2−x)(3x−1)24(1−a)2≥0(vì )<a<1)
⇒a2(1−a)2≥9a−24
tương tự: b2(1−b)2≥9b−24
⇒P⩾49(9a−24+9b−24)−3(a+b)24=(a+b)−94−3(a+b)24.
đặt t=a+b(0<t<1)⇒P≥F(t)=−3t24+t−94(∗)
Xét hàm (∗) được: MinF(t)=F(23)=−19
⇒MinP=MinF(t)=−19.dấu "=" xảy ra khi a=b=c=13
Ta có: \(\frac{a}{1+b^2}=\frac{a\left(1+b^2\right)-ab^2}{1+b^2}=a-\frac{ab}{1+b^2}\)
\(1+b^2\ge2b\) \(\Rightarrow\frac{ab^2}{1+b^2}\le\frac{ab^2}{2b}=\frac{ab}{2}\)\(\Rightarrow-\frac{ab^2}{1+b^2}\ge-\frac{ab}{2}\)
Do đó: \(\frac{a}{1+b^2}=a-\frac{ab^2}{1+b^2}\ge a-\frac{ab}{2}\)
Tương tự: \(\frac{b}{1+c^2}\ge b-\frac{bc}{2}\); \(\frac{c}{1+a^2}\ge c-\frac{ca}{2}\)
Suy ra \(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2}+\frac{ab+bc+ca}{2}\ge a+b+c\)
Mặt khác ta có: \(3\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\Rightarrow\frac{3}{a+b+c}\le1\)
\(\Rightarrow a+b+c\ge3\)
Do đó; \(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2}+\frac{ab+bc+ca}{2}\ge a+b+c\ge3\)(đpcm)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=1\)
Ta có: \(\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{1}{b}\)
\(\Rightarrow bc+ca=2ca\)
\(P=\dfrac{a+b}{2a-b}+\dfrac{c+b}{2c-b}=\dfrac{ac+bc}{2ca-bc}+\dfrac{ca+ab}{2ca-ab}\)
\(=\dfrac{ca+bc}{ab}+\dfrac{ca+ab}{bc}=\dfrac{c}{b}+\dfrac{c}{a}+\dfrac{a}{b}+\dfrac{a}{c}=\dfrac{c+a}{b}+\dfrac{c}{a}+\dfrac{a}{c}\)
Ta có :
\(\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{1}{c}\ge\dfrac{4}{a+c}\left(\text{Svácxơ}\right)\)\(\Rightarrow c+a\ge2b\)
Áp dụng bđt cô si cho 2 số dương
\(\dfrac{c}{a}+\dfrac{a}{c}\ge2\sqrt{\dfrac{c}{a}.\dfrac{a}{c}}=2\)
\(\Rightarrow P\ge\dfrac{2b}{b}+2=4\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c\)
Chú ý đến giả thiết a + b + c = 1 ta viết được \(\frac{ab}{\sqrt{\left(1-c\right)^3\left(1+c\right)}}=\frac{ab}{\sqrt{\left(a+b\right)^2\left(1-c\right)\left(1+c\right)}}=\)\(\frac{ab}{\left(a+b\right)\sqrt{1-c^2}}=\frac{ab}{\left(a+b\right)\sqrt{\left(a+b+c\right)^2-c^2}}\)\(=\frac{ab}{\left(a+b\right)\sqrt{a^2+b^2+2\left(ab+bc+ca\right)}}\)
Mặt khác áp dụng bất đẳng thức Cauchy ta được \(a^2+b^2+2\left(ab+bc+ca\right)\ge2ab+2\left(ab+bc+ca\right)=\)\(2\left(ab+bc\right)+2\left(ab+ca\right)\)và \(a+b\ge2\sqrt{ab}\)
Từ đó dẫn đến \(\frac{ab}{\left(a+b\right)\sqrt{a^2+b^2+2\left(ab+bc+ca\right)}}\le\frac{ab}{2\sqrt{ab}\sqrt{2\left(ab+bc\right)+2\left(ab+ca\right)}}\)\(=\frac{1}{2}\sqrt{\frac{ab}{2\left(ab+bc\right)+2\left(ab+ca\right)}}\)
Mà theo bất đẳng thức quen thuộc \(\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)\) ta có: \(\sqrt{\frac{ab}{2\left(ab+bc\right)+2\left(ab+ca\right)}}\le\sqrt{\frac{1}{4}\left(\frac{ab}{2\left(ab+bc\right)}+\frac{ab}{2\left(ab+ca\right)}\right)}\)
\(=\frac{1}{2\sqrt{2}}\sqrt{\frac{ab}{ab+bc}+\frac{ab}{ab+ca}}=\frac{1}{2\sqrt{2}}\sqrt{\frac{a}{a+c}+\frac{b}{b+c}}\)
Từ đó ta có bất đẳng thức: \(\frac{ab}{\sqrt{\left(1-c\right)^3\left(1+c\right)}}\le\frac{1}{4\sqrt{2}}\sqrt{\frac{a}{a+c}+\frac{b}{b+c}}\)(1)
Hoàn toàn tương tự, ta có: \(\frac{bc}{\sqrt{\left(1-a\right)^3\left(1+a\right)}}\le\frac{1}{4\sqrt{2}}\sqrt{\frac{b}{b+a}+\frac{c}{c+a}}\)(2) ; \(\frac{ca}{\sqrt{\left(1-b\right)^3\left(1+b\right)}}\le\frac{1}{4\sqrt{2}}\sqrt{\frac{c}{c+b}+\frac{a}{a+b}}\)(3)
Cộng theo vế 3 bất đẳng thức (1), (2), (3), ta được: \(\frac{ab}{\sqrt{\left(1-c\right)^3\left(1+c\right)}}+\frac{bc}{\sqrt{\left(1-a\right)^3\left(1+c\right)}}+\frac{ca}{\sqrt{\left(1-b\right)^3\left(1+b\right)}}\)\(\le\frac{1}{4\sqrt{2}}\left(\sqrt{\frac{a}{a+c}+\frac{b}{b+c}}+\sqrt{\frac{b}{b+a}+\frac{c}{c+a}}+\sqrt{\frac{c}{c+b}+\frac{a}{a+b}}\right)\)
Ta cần chứng minh\(\frac{1}{4\sqrt{2}}\left(\sqrt{\frac{a}{a+c}+\frac{b}{b+c}}+\sqrt{\frac{b}{b+a}+\frac{c}{c+a}}+\sqrt{\frac{c}{c+b}+\frac{a}{a+b}}\right)\le\frac{3\sqrt{2}}{8}\)
Hay \(\sqrt{\frac{a}{a+c}+\frac{b}{b+c}}+\sqrt{\frac{b}{b+a}+\frac{c}{c+a}}+\sqrt{\frac{c}{c+b}+\frac{a}{a+b}}\le3\)
Áp dụng bất đẳng thức Bunhiacopxki ta được \(\sqrt{\frac{a}{a+c}+\frac{b}{b+c}}+\sqrt{\frac{b}{b+a}+\frac{c}{c+a}}+\sqrt{\frac{c}{c+b}+\frac{a}{a+b}}\)
\(\le\sqrt{3\left(\frac{a}{a+c}+\frac{b}{b+c}+\frac{b}{b+a}+\frac{c}{c+a}+\frac{c}{c+b}+\frac{a}{a+b}\right)}=3\)
Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra khi \(a=b=c=\frac{1}{3}\)
Sửa đề: \(\frac{ca}{\sqrt{\left(1-b\right)^3\left(1+b\right)}}\)