IT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 10 2016
Bạn tự vẽ hình nhé !
Gọi\(\Delta ABC\)đều có O vừa là tâm đường tròn ngoại tiếp vừa là trọng tâm ; AH vừa là đường cao vừa là trung tuyến
=> HB = BC/2 = 3/2 = 1,5 (cm) =>\(\Delta AHB\)vuông tại H có :\(AH=\sqrt{AB^2-BH^2}=\sqrt{3^2-\left(1,5\right)^2}=\frac{3\sqrt{3}}{2}\left(cm\right)\)
=> Bán kính đường tròn ngoại tiếp là : AO =\(\frac{2}{3}.AH=\frac{2}{3}.\frac{3\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)(vì O là trọng tâm)
CM
4 tháng 1 2017
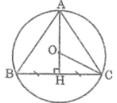
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
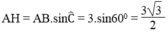
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
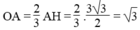
Vậy chọn đáp án C.
NN
3
9 tháng 9 2021
Bán kính đường tròn ngoại tiếp của ΔABC là:
R=a√3 / 3=4√3 / 3(cm)
NN
0
CM
10 tháng 6 2017
Gọi O là giao 3 đường trung trực của ∆ABC. Khi đó O là tâm đường tròn ngoại tiếp ∆ABC. Gọi H là giao điểm của AO và BC. Ta có : AH = 3 cm
OA = 2 3 AH = 2 3 3 cm
ND
0
PT
1
CM
11 tháng 9 2018
Theo bài 46 ta có:
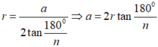
Áp dụng vào hình ngũ giác đều ngoại tiếp đường tròn bán kính 3cm ta có:
7 tháng 9 2023
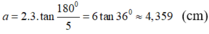
ΔABC đều nên chiều cao của nó là \(3\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}\)
Bán kính của đường tròn ngoại tiếp là: \(3\cdot\dfrac{\sqrt{3}}{3}=\sqrt{3}\)
\(R=\dfrac{a\sqrt{3}}{3}=\sqrt{3}\left(cm\right)\)