Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x+2y-5=0\\4x+13y-10=0\end{matrix}\right.\) \(\Rightarrow A\left(9;-2\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-5;5\right)=5\left(-1;1\right)\)
Phương trình AC: \(1\left(x-4\right)+1\left(y-3\right)=0\Leftrightarrow x+y-7=0\)
Phương trình đường thẳng qua C vuông góc AD có dạng:
\(2\left(x-4\right)-1\left(y-3\right)=0\Leftrightarrow2x-y-5=0\)
Gọi E là hình chiếu của C lên AD \(\Rightarrow\left\{{}\begin{matrix}2x-y-5=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow E\left(3;1\right)\)
Gọi F là điểm đối xứng C qua AD \(\Rightarrow F\) thuộc AB đồng thời E là trung điểm CF \(\Rightarrow F\left(2;-1\right)\)
\(\overrightarrow{AF}=\left(-7;1\right)\Rightarrow\) pt AB: \(1\left(x-2\right)+7\left(y+1\right)=0\Leftrightarrow x+7y+5=0\)
Tọa độ B có dạng: \(B\left(-7b-5;b\right)\) \(\Rightarrow M\left(\dfrac{-7b-1}{2};\dfrac{b+3}{2}\right)\)
M thuộc AM nên: \(4\left(\dfrac{-7b-1}{2}\right)+13\left(\dfrac{b+3}{2}\right)-10=0\Rightarrow b=1\Rightarrow B\left(-12;1\right)\)
\(\Rightarrow\overrightarrow{BC}\Rightarrow\) phương trình BC
Tính độ dài 3 cạnh, tính diện tích theo công thức Hê-rông
Bạn tự hoàn thành phần còn lại nhé
Đặt \(\left\{{}\begin{matrix}\frac{1}{x+3y-1}=X\\\frac{1}{2x-y+3}=Y\end{matrix}\right.\)
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2X-Y=5\\X+2Y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4X-2Y=10\\X+2Y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5X=15\\X+2Y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}X=3\\Y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{1}{x+3y-1}=3\\\frac{1}{2x-y+3}=1\end{matrix}\right.\) (nhân chéo) \(\Leftrightarrow\left\{{}\begin{matrix}x+3y-1=\frac{1}{3}\\2x-y+3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\frac{4}{3}\\2x-y=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\frac{4}{3}\\6x-3y=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\frac{4}{3}\\7x=-\frac{14}{3}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\frac{2}{3}\\y=\frac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(-\frac{2}{3};\frac{2}{3}\right)\)
a: vecto AB=(1;-1)
=>VTPT là (1;1)
Phương trình AB là:
1(x-0)+1(y-3)=0
=>x+y-3=0
vecto AC=(-3;2)
=>VTPT là (2;3)
Phương trình AC là:
2(x-0)+3(y-3)=0
=>2x+3y-9=0
vecto BC=(-4;3)
=>VTPT là (3;4)
Phương trình BC là;
3(x-1)+4(y-2)=0
=>3x-3+4y-8=0
=>3x+4y-11=0
vecto BC=(-4;3)
=>AH có VTPT là (-4;3)
Phương trình AH là;
-4(x-0)+3(y-3)=0
=>-4x+3y-9=0
b: vecto AC=(-3;2)
=>BK có VTPT là (-3;2)
Phương trình BK là:
-3(x-1)+2(y-2)=0
=>-3x+3+2y-4=0
=>-3x+2y-1=0
Tọa độ K là:
-3x+2y-1=0 và -4x+3y-9=0
=>K(15;23)
d: vecto AB=(1;-1)
=>Đường trung trực của AB có VTPT là (1;-1)
Tọa độ N là trung điểm của AB là:
x=(0+1)/2=1/2 và y=(2+3)/2=2,5
Phương trình đường trung trực của AB là:
1(x-0,5)+(-1)(y-2,5)=0
=>x-y+2=0
a) Phương trình đường thẳng AB đi qua 2 điểm A và B là: \(\frac{{x - 1}}{{ - 1 - 1}} = \frac{{y - 3}}{{ - 1 - 3}} \Leftrightarrow \frac{{x - 1}}{{ - 2}} = \frac{{y - 3}}{{ - 4}} \Leftrightarrow 2x - y + 1 = 0\)
Phương trình đường thẳng AC đi qua 2 điểm A và C là: \(\frac{{x - 1}}{{5 - 1}} = \frac{{y - 3}}{{ - 3 - 3}} \Leftrightarrow \frac{{x - 1}}{4} = \frac{{y - 3}}{{ - 6}} \Leftrightarrow 3x + 2y - 9 = 0\)
Phương trình đường thẳng BC đi qua 2 điểm B và C là:
\(\frac{{x + 1}}{{5 + 1}} = \frac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow \frac{{x + 1}}{6} = \frac{{y + 1}}{{ - 2}} \Leftrightarrow x + 3y + 4 = 0\)
b) Gọi d là đường trung trực của cạnh AB.
Lấy N là trung điểm của AB, suy ra \(N\left( {0;1} \right)\).
Do \(d \bot AB\) nên ta có vecto pháp tuyến của d là: \(\overrightarrow {{n_d}} = \left( {1;2} \right)\)
Vậy phương trình đường thẳng d đi qua N có vecto pháp tuyến \(\overrightarrow {{n_d}} = \left( {1;2} \right)\) là:
\(1\left( {x - 0} \right) + 2\left( {y - 1} \right) = 0 \Leftrightarrow x + 2y - 2 = 0\)
c) Do AH vuông góc với BC nên vecto pháp tuyến của AH là \(\overrightarrow {{n_{AH}}} = \left( {3; - 1} \right)\)
Vậy phương trình đường cao AH đi qua điểm A có vecto pháp tuyến \(\overrightarrow {{n_{AH}}} = \left( {3; - 1} \right)\)là: \(3\left( {x - 1} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow 3x - y = 0\)
Do M là trung điểm BC nên \(M\left( {2; - 2} \right)\). Vậy ta có: \(\overrightarrow {AM} = \left( {1; - 5} \right) \Rightarrow \overrightarrow {{n_{AM}}} = \left( {5;1} \right)\)
Phương trình đường trung tuyến AM đi qua điểm A có vecto pháp tuyến \(\overrightarrow {{n_{AM}}} = \left( {5;1} \right)\) là:
\(5\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 5x + y - 8 = 0\)
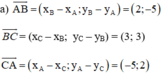
+ Lập phương trình đường thẳng AB:
Đường thẳng AB nhận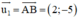 
là 1 vtcp ⇒ AB nhận 
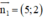là 1 vtpt
Mà A(1; 4) thuộc AB
⇒ PT đường thẳng AB: 5(x- 1) + 2(y – 4) = 0 hay 5x + 2y – 13 = 0.
+ Lập phương trình đường thẳng BC:
Đường thẳng BC nhận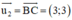 
là 1 vtcp ⇒ BC nhận 
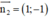là 1 vtpt
Mà B(3; –1) thuộc BC
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y + 1) = 0 hay x – y – 4 = 0.
+ Lập phương trình đường thẳng CA:
Đường thẳng CA nhận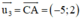 
là 1 vtcp ⇒ CA nhận 
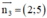là 1 vtpt
Mà C(6; 2) thuộc CA
⇒ Phương trình đường thẳng AC: 2(x – 6) + 5(y - 2) = 0 hay 2x + 5y – 22 = 0.
b) + AH là đường cao của tam giác ABC ⇒ AH ⊥ BC
⇒ Đường thẳng AH nhận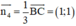 
là 1 vec tơ pháp tuyến
Mà A(1; 4) thuộc AH
⇒ Phương trình đường thẳng AH: 1(x - 1) + 1(y - 4) = 0 hay x + y – 5 = 0.
+ Trung điểm M của BC có tọa độ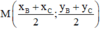 
hay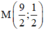 
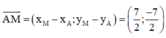
Đường thẳng AM nhận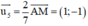 
là 1 vtcp
⇒ AM nhận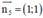 
là 1 vtpt
Mà A(1; 4) thuộc AM
⇒ Phương trình đường thẳng AM: 1(x - 1) + 1(y – 4) = 0 hay x + y – 5 = 0.
a.
\(\overrightarrow{AB}=\left(4;-2\right)=2\left(2;-1\right)\Rightarrow\) đường thẳng AB nhận (2;-1) là 1 vtcp
Phương trình AB (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+2t\\y=2-t\end{matrix}\right.\)
\(\overrightarrow{CB}=\left(5;-1\right)\Rightarrow\) đường thẳng BC nhận (5;-1) là 1 vtcp
Phương trình BC (qua C) có dạng: \(\left\{{}\begin{matrix}x=5t_1\\y=1-t_1\end{matrix}\right.\)
\(\overrightarrow{CA}=\left(1;1\right)\Rightarrow\) đường thẳng AC nhận (1;1) là 1 vtcp
Phương trình AC (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+t_2\\y=2+t_2\end{matrix}\right.\)
b.
Gọi M là trung điểm BC \(\Rightarrow M\left(\dfrac{5}{2};\dfrac{1}{2}\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(\dfrac{3}{2};-\dfrac{3}{2}\right)=\dfrac{3}{2}\left(1;-1\right)\)
\(\Rightarrow\) Đường thẳng AM nhận (1;-1) là 1 vtcp
Phương trình AM (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+t_3\\y=2-t_3\end{matrix}\right.\)
c.
Đường thẳng AH vuông góc BC nên nhận (1;5) là 1 vtcp
Phương trình AH (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+t_4\\y=2+5t_4\end{matrix}\right.\)
d.
Trung trực AB vuông góc AB nên nhận (1;2) là 1 vtcp
Gọi N là trung điểm AB \(\Rightarrow N\left(3;1\right)\)
Trung trực AB đi qua N và có vtcp là (1;2) nên pt có dạng:
\(\left\{{}\begin{matrix}x=3+t_5\\y=1+2t_5\end{matrix}\right.\)
Cách làm: Tính độ dài các đoạn AB,AC,BC
Do AD là phân giác trong nên D nằm giữa B và C
⇒ \(\overrightarrow{BD}\uparrow\uparrow\overrightarrow{BC}\)
Tính chất đường phân giác
⇒ \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
⇒ \(\dfrac{AB}{AC}=\dfrac{BD}{BC-BD}\)
⇒ \(\dfrac{AB}{AB+AC}.BC=BD\)
⇒ \(\dfrac{AB}{AB+AC}.\overrightarrow{BC}=\overrightarrow{BD}\)
⇒ Tọa độ điểm D
Phương trình đường thẳng AD là phương trình đi qua 2 điểm
A (-6;-3) và D(x;y)
\(A\left(-6;-3\right),B\left(-4;3\right),C\left(9;2\right)\)
\(\Rightarrow AB=2\sqrt{10};AC=5\sqrt{10}\)
\(\overrightarrow{BC}=\left(13;-1\right)\) \(\Rightarrow\) VTPT của đường thẳng BC là \(\overrightarrow{n}=\left(1;13\right)\)
\(\Rightarrow\) PTTQ của BC là: \(1\left(x+4\right)+13\left(y-3\right)=0\Leftrightarrow x+13y-35=0\)
Do \(D\in BC\Rightarrow D\left(-13y+35;y\right)\)
Do \(AD\) là phân giác của \(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{2\sqrt{10}}{5\sqrt{10}}=\dfrac{2}{5}\) \(\Rightarrow5DB=2DC\)
\(\Rightarrow5\sqrt{\left(-13y+39\right)^2+\left(y-3\right)^3}=2\sqrt{\left(-13y+26\right)^2+\left(y-2\right)^2}\)
\(\Rightarrow5\left|y-3\right|\sqrt{13^2+1}=2\left|y-2\right|\sqrt{13^2+1}\)
\(\Rightarrow5\left|y-3\right|=2\left|y-2\right|\)
Giải phương trình trên ta được \(y=\dfrac{19}{7}\Rightarrow D\left(-\dfrac{2}{7};\dfrac{19}{7}\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(\dfrac{40}{7};\dfrac{40}{7}\right)=\dfrac{40}{7}\left(1;1\right)\)
\(\Rightarrow\) VTPT của AD là \(\left(1;-1\right)\)
\(\Rightarrow\) Phương trình AD: \(1\left(x+6\right)-1\left(y+3\right)=0\Leftrightarrow x-y+3=0\).