Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A) Xet tam giac abh va tam giac ach
ah=ah (canh chung)
hb=hc vi trung diem
ab=ac vi tam giac abc can tai a
B)xet tam giac aeh vuong tai e va tam giac afh vuong tai f
eah=fah vi tam giac ahb=tam giac ahc
ah=ah canh chung
>> he=hf
C) xet tam giac aef
ae=af vi tam giac aeh=tam giac afh
>>tam giac aef can tai a
ta co
Goc aef=(180-goc aef):2( tam giac aef can taia)
Goc abc=(180-goc bac):2 (tam giac abc can tai a)
goc aef=goc bac( goc chung)
>>goc aef=goc abc
ma goc aef va goc abc nam o vi tri dong vi
>>ef//bc

a, xét tam giác AHB và tg AHC có : ^AHC = ^AHB = 90
AB = AC do tg ABC cân tại A (gt)
^ABC = ^ACB do tg ABC ...
=> tg AHB = tg AHC (ch-gn)
b, tg ABC cân tại A (Gt) mà có AH là đường cao (1)
=> AH đồng thời là đường trung tuyến
=> H là trung điểm của BC
=> BH = 1/2BC = 6 cm
tg AHB vuông tại H (gt) => AB^2 = AH^2 + HB^2 (ĐL pytago)
AB = 10 (gt)
=> AH = 8 do AH > 0
c, (1) => AH đồng thời là pg của ^BAC (đl)
=> ^CAH = ^BAH (đn)
có HE // AC (gt) ; ^CAH slt ^AHE => ^CAH = ^AHE (đl)
=> ^BAH = ^AHE
=> tg AHE cân tại E (dh)

ghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
mấy bạn bớt nhắn linh tinh lên đây đi, olm là nơi học bài và hỏi bài chứ không phải nhắn lung tung

a;
có Abc là tam giac cân taji A (gt)
=> AH là đg cao và là ddg trùng tuyến và là đg phan giác
=> H là trung điểm của BC
Xét tam giác ABH va ACH có
1: có AH chung
2: HB=HC( CMT)
3: AB=AC (2 cạnh bên của tam giác ABC cân tại a)
=> 2 tam giác bằng nhau theo TH c.c.c
b;
xét 2 tam giác: AMB va CME có
AM=MC ( BM là trung tuyến=>m là trung điểm AC)
MB=ME (GT)
Góc AMB=Goc AMC (2 góc đối đỉnh)
=> 2tam giác bằng nhau theo TH (CGC)
=> góc CEm= góc ABM (2 góc tương ung trong 2 tam giác bằng nhau)
=> AB//CE (2 đg thằng có 2 góc đồng vị bằng nhau)
c;
có AB//CE (CMt)
=> Góc ABC= góc BCK (2 góc so le trong)
xet 2 tam giác vuông ACH va KCH có
HC chung
goc KCH=ACH (cùng bằng góc ABC)
=> 2 tam giác bằng nhau
=>HK=AH (1)
xet Tam gioác ABC có am là trung tuyên tại M; BM là trung tuyến
=> G là trọng tâm
=> HG= 1/3 AH (tinh chât trọng tâm của tam giác) (2)
tù 1 và 2 => HG=1/3 HK => HK=3HG(3)
Trong Tam giác KHC có
CK< HC+HK (4)
Từ 3 và 4 => KC< HC+3HG (dieu phai chung minh)
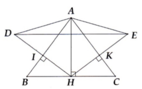



a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xet ΔAEH vuông tại E và ΔAKH vuông tại K có
AH chung
góc EAH=góc KAH
=>ΔAEH=ΔAKH
=>AE=AK