DH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A4
2
NH
6 tháng 4 2023
a)
`a<b`
`<=>3a<3b`
`<=>3a-5<3b-5`
b)
`a<b`
`<=>-8a> -8b`
`<=>-8a-3> -8b-3`
c)
`a<b`
`<=>4a<4b`
`<=>4a+9<4b+9`
mà `4a-7<4a+9`
`<=>4a-7<4b+9`
BV
0
16 tháng 12 2016
có thể là bé hơn hoặc bằng,các bạn thử cho mình với nhé
17 tháng 8 2020
áp dụng Bất Đẳng Thức CBS \(\sqrt{3a^2+8b^2+14ab}=\sqrt{\left(a+4b\right)\left(3a+2b\right)}\le\frac{1}{2}\left(4a+6b\right)\)
(BĐT CBS) do đó ta \(\Rightarrow\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\frac{a^2}{2a+3b}\)
tương tư với mẫu còn lại
\(\Rightarrow\Sigma\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\Sigma\frac{a^2}{2a+3b}\ge\frac{\left(a+b+c\right)^2}{5\left(a+b+c\right)}=\frac{a+b+c}{5}\left(Q.E.D\right)\)
đẳng thức xảy ra khi a=b=c
KB
26 tháng 2 2019
Đặt PT đã cho ở đề là A
Ta có : \(\sqrt{3a^2+8b^2+14ab}=\sqrt{3a\left(a+4b\right)+2b\left(a+4b\right)}=\sqrt{\left(3a+2b\right)\left(a+4b\right)}\)
\(\le\dfrac{3a+2b+a+4b}{2}=\dfrac{4a+6b}{2}=2a+3b\)
\(\Rightarrow\dfrac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\dfrac{a^2}{2a+3b}\)
Làm tương tự như trên , ta có :
\(\dfrac{b^2}{\sqrt{3b^2+8c^2+14bc}}\ge\dfrac{b^2}{2b+3c};\dfrac{c^2}{\sqrt{3c^2+8a^2+14ac}}\ge\dfrac{c^2}{2c+3a}\)
Nên : \(A\ge\dfrac{a^2}{2a+3b}+\dfrac{b^2}{2b+3c}+\dfrac{c^2}{2c+3a}\ge\dfrac{\left(a+b+c\right)^2}{5\left(a+b+c\right)}=\dfrac{5}{a+b+c}\left(đpcm\right)\)
8 tháng 12 2017
Chứng minh BĐT phụ: \(\frac{m^2}{x}+\frac{n^2}{y}\ge\frac{\left(m+n\right)^2}{x+y}\) với \(x;y>0\) (*)
Ta có: \(3a^2+8b^2+14ab\)
\(=\left(3a^2+12ab\right)+\left(2ab+8b^2\right)\)
\(=3a\left(a+4b\right)+2b\left(a+4b\right)\)
\(=\left(3a+2b\right)\left(a+4b\right)\)
\(\Rightarrow\sqrt{3a^2+8b^2+14ab}=\sqrt{\left(3a+2b\right)\left(a+4b\right)}\le\frac{3a+2b+a+4b}{2}=2a+3b\)
\(\Rightarrow\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\frac{a^2}{2a+3b}\)
Tương tự, ta có: \(\frac{b^2}{\sqrt{3b^2+8c^2+14bc}}\ge\frac{b^2}{2b+3c}\)
\(\frac{c^2}{\sqrt{3c^2+8a^2+14ca}}\ge\frac{c^2}{2c+3a}\)
Áp dụng (*), ta có:
\(VT\ge\frac{a^2}{2a+3b}+\frac{b^2}{2b+3c}+\frac{c^2}{2c+3a}\ge\frac{\left(a+b+c\right)^2}{2a+3b+2b+3c+2c+3a}=\frac{\left(a+b+c\right)^2}{5\left(a+b+c\right)}\)
\(=\frac{1}{5}\left(a+b+c\right)\)
Vậy \(\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}+\frac{b^2}{\sqrt{3b^2+8c^2+14bc}}+\frac{c^2}{\sqrt{3c^2+8a^2+14ca}}\ge\frac{1}{5}\left(a+b+c\right)\)
6 tháng 8 2020
Bài 1
Gọi số học sinh lớp 8A là x (học sinh) ĐK: x ∈ N* và x < 80
Số học sinh lớp 8B là 80 - x(học sinh)
Số sách lớp 8A ủng hộ là 2x (quyển)
Số sách lớp 8B ủng hộ là 3(80 - x) (quyển)
Theo bài ta có phương trình:
<=>2x + 3(80 - x) = 198
<=>2x + 248 - 3x = 198
x = 42 (thoả mãn điều kiện) Vậy số học sinh lớp 8A là 42 học sinh,số học sinh lớp 8B là 38 học sinh.
Bài 2
Gọi độ dài quãng đường AB là x (km) (ĐK: x > 0)
Thời gian lúc đi là: x/35 (giờ), thời gian lúc về là : x/42 (giờ).
Theo bài ra ta có phương trình: x/35 - x/42 = 1/2
Giải phương trình được x = 105, thoả mãn điều kiện của ẩn. Trả lời : Vậy độ dài quãng đường AB là 105 km.
Hok tốt ^^
6 tháng 8 2020
Bài 1: Gọi x (h/s) là số h/s của lớp 8A (0 < x < 80 ). Số h/s của lớp 8D là: 80 - x
Số cách lớp 8a ủng hộ là 2x (quyển); số sách lớp 8D ủng hộ là 3(80 - x) (quyển)
Theo đề bài 2 lớp góp đc 198 nên ta có phương trình: 2x +3(80 - x) = 198
<=> 2x + 240 - 3x = 198 => x = 42 (h/s) (TMĐK) => Số h/s lớp 8A là: 42 h/s
Số h/s lớp 8D là: 80 - x = 80 - 24 = 56 (h/s)
Bài 2: Gọi t(h) là thời gian đi (t > 0,5) - quãng đường AB (tính theo lúc đi) 35t
- quãng đường AB (tính theo lúc về) 42(t - 0,5)
Ta có phương trình: 35t = 42(t - 0,5) giải phương trình: 35t = 42(t-0,5)
<=> 35t = 42t - 21 <=> -7t = -21 <=> t = 3
=> Quãng đường AB dài là: 35.3 = 105 (km)
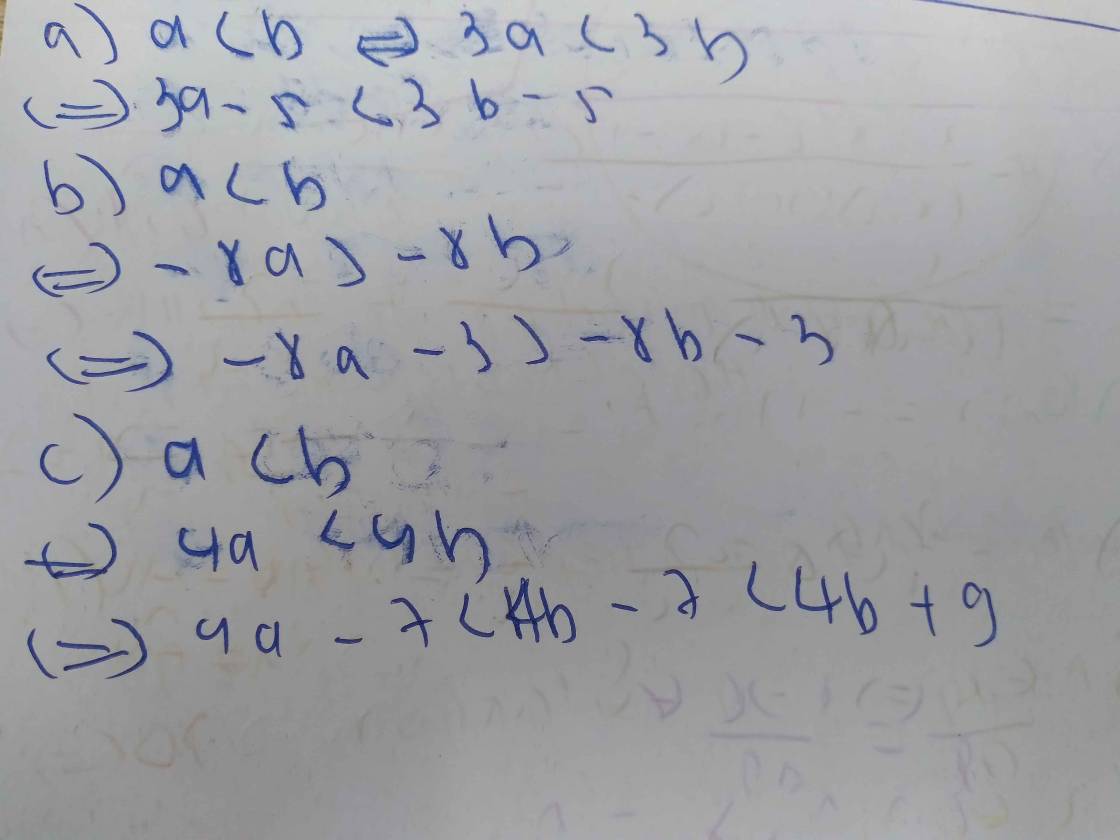
a) Vì a>b
=>3a>3b
=>5-3a<5-3b
c) vì a>b
=>8a>8b
=>8a-3>8b-3
c) vì a>b
=>8a>8b
Vì 3<5
=>8a-3<8b-5