Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB và OH là phân giác của \(\widehat{AOB}\)
ta có: OH là phân giác của góc AOB
=>OM là phân giác của góc AOB
=>\(\widehat{AOM}=\widehat{BOM}\)
Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
=>\(\widehat{OBM}=\widehat{OAM}\)
mà \(\widehat{OAM}=90^0\)
nên \(\widehat{OBM}=90^0\)
=>MB là tiếp tuyến của (O)
b: Sửa đề: B,O,C thẳng hàng
Ta có: AB\(\perp\)OM
OM//AC
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
Vì ΔABC vuông tại A
nên ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
c: Xét (O) có
ΔDBC nội tiếp
BC là đường kính
Do đó: ΔDBC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)CM tại D
Xét ΔBCM vuông tại B có BD là đường cao
nên \(MD\cdot MC=MB^2\)(1)
Xét ΔBOM vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MC=MH\cdot MO\)
=>\(\dfrac{MD}{MO}=\dfrac{MH}{MC}\)
Xét ΔMDH và ΔMOC có
\(\dfrac{MD}{MO}=\dfrac{MH}{MC}\)
\(\widehat{DMH}\) chung
Do đó: ΔMDH đồng dạng với ΔMOC
=>\(\widehat{MHD}=\widehat{MCO}\)
=>\(\widehat{MHD}=\widehat{OCD}\)
mà \(\widehat{OCD}=\widehat{ODC}\)(ΔOCD cân tại O)
nên \(\widehat{MHD}=\widehat{ODC}\left(3\right)\)
Ta có: \(\widehat{MHD}=\widehat{MCO}\)
mà \(\widehat{MHD}+\widehat{OHD}=180^0\)(hai góc kề bù)
nên \(\widehat{MCO}+\widehat{OHD}=180^0\)
=>\(\widehat{OCD}+\widehat{OHD}=180^0\)
=>OHDC là tứ giác nội tiếp
=>\(\widehat{OHC}=\widehat{ODC}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{OHC}=\widehat{MHD}\)

a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
b: Xét (O) có
ΔBAD nôi tiếp
BD là đường kính
Do đó:ΔBAD vuông tại A
=>AD vuông góc với BA
=>AD//CB

a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
Suy ra: \(\widehat{OAC}=\widehat{OBC}=90^0\)
hay BC là tiếp tuyến của (O)
b: Xét (O) có
ΔABD nội tiếp
BD là đường kính
Do đó: ΔABD vuông tại A
Suy ra: BA⊥AD
mà AB⊥OC
nên AD//OC

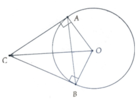
a, ∆OAC = ∆OBC (c.g.c)
=> O B C ^ - O A B ^ = 90 0
=> đpcm
b, Sử dụng hệ thức lượng trong tam giác vuông OBC tính được OC=25cm

tạm thời mình làm a trước nhá
nối d với O ta có OD=OB=OA=R
=>tam giác AOD vuông
=>AD VUÔNG GÓC VỚI BM

1: ΔOAB cân tại O
mà OM là đường cao
nên OM là trung trực của AC
=>OC là trung trực của AB
2: ΔOAB cân tại O
mà OM là đường cao
nên OM là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
3: Sửa đề: CM AD//OC
Xét (O) có
góc DAB là góc nội tiếp chắn nửa đường tròn
=>góc DAB=90 độ
=>DA vuông góc AB
=>DA//OC