Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A) Xét tam giác BEC và tam giác CDB có :
\(\widehat{BEC}\)=\(\widehat{CDB}\)=\(90^0\)
\(BC\)chung
\(\widehat{EBC}\)=\(\widehat{DCB}\)( giả thiết )
\(\Rightarrow\Delta EBC=\Delta DCB\left(G-C-G\right)\)
Vậy \(BD=CE\) ( hai canh tương ứng )
B) Xét tam giác DHC và tam giác EHC có :
\(\widehat{EBH}\) =\(\widehat{DCH}\)( vì góc CDH=góc BEB ; góc EHB = góc DHC )
EB=DC ( theo phần a )
\(\widehat{HEB}\)=\(\widehat{CDH}\)=900
\(\Rightarrow\)\(\Delta EHB=\Delta DHC\left(G-C-G\right)\)
\(\Rightarrow BB=HC\)( HAI CẠNH TƯƠNG ỨNG )
\(\Rightarrow\Delta BHC\)cân ( định lí tam giác cân )
C) Ta có : AB =AC ( giả thiêt )
Vậy góc A cách đều hai mút B và C
Vậy AH là đường trung trực của BC
d)Xét tam giác BDC và tam giác KDC có :
DK=DB ( GT )
CD ( chung )
suy ra tam giác BDC =tam giác KDC ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\) \(\widehat{BCD}\)=\(\widehat{KCD}\)( HAI GÓC TƯƠNG ỨNG )
Mà ta lai có góc EBC = góc BCD theo giả thiết )
\(\Rightarrow\)\(\widehat{EBC}\)=\(\widehat{EBC}\)
chúc bạn hok giỏi

a. xét tam giác ABD và tam giác ACE có
BDA=CEA=90 độ
AB=AC (do tam giác ABC cân tai A)
Chung góc A
Suy ra: tam giác ABD= tam giác ACE
Suy ra: BD=CE (hai cạnh tương ứng)

tự kẻ hình
a) xét tam giác BEC và tam giác CDB có
BC chung
BEC=CDB(=90 độ)
ABC=ACB( tam giác ABC cân A)
=> tam giác BEC= tam giác CDB(ch-gnh)
=> BD=CE( hai cạnh tương ứng)
b) từ tam giác BEC= tam giác CDB=> DBC=ECB(hai góc tương ứng)
=> tam giác HBC cân H
c) đặt O là giao điểm của AH với BC
vì AH,BD,CE cùng giao nhau tại H mà BD, CE là đường cao=> AH là đường cao ( 3 đường cao cùng đi qua một điểm)
vì HBC cân H=> HB=HC
xét tam giác HOB và tam giác HOC có
HB=HC(cmt)
HBO=HCO(cmt)
HOB=HOC(=90 độ)
=> tam giác HOB= tam giác HOC(ch-gnh)
=> BO=CO( hai cạnh tương ứng)
=> AH là trung trực của BC
d) xét tam giác CDB và tam giác CDK có
BD=DK(gt)
CDB=CDK(=90 độ)
DC chung
=> tam giác CDB= tam giác CDK(cgc)
=> CBD=CKD( hai cạnh tương ứng)
mà CBD=BCE=> CKD=BCE

Nguyễn Diệu Linh.

Cho tam giác ABC cân tại A (góc A < 90 độ). Kẻ BD vuông góc AC (D thuộc AC), CE vuông góc AB (E thuộc AB), BD và CE cắt nhau tại H. a) Chứng minh BD = CE. b) Chứng minh tam giác BHC cân. c) Chứng minh AH là đường trung trực của BC. d) Trên tia BD lấy điểm K sao cho D là trung điểm của BK. So sánh góc ECB và góc DKC - Toán học Lớp 7 - Bài tập Toán học Lớp 7 - Giải bài tập Toán học Lớp 7 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
cho hình chữ nhật ABCD ,đường chéo BD.Từ A ve AH vuong goc BD(H thuocB) a)CM tam giac HAD dong dang tam giac CDB b)CM AH.BD=AD.AB c) cho BH=9cm,HD=16cm.Tinh dien h tam giac ABC.
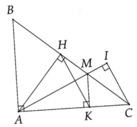

b) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
Xét ΔIBH vuông tại H và ΔICH vuông tại H có
BH=CH(cmt)
IH chung
Do đó: ΔIBH=ΔICH(hai cạnh góc vuông)
Suy ra: IB=IC(hai cạnh tương ứng)
Xét ΔIBC có IB=IC(cmt)
nên ΔIBC cân tại I(Định nghĩa tam giác cân)
Ta có: ΔIKC vuông tại K(gt)
nên IC là cạnh lớn nhất(Do IC là cạnh huyền)
hay IK<IC
mà IB=IC(cmt)
nên IK<IB
c) Ta có: ΔKBC vuông tại K(gt)
nên \(\widehat{KBC}+\widehat{KCB}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{KBC}+\widehat{ACB}=90^0\)(1)
Ta có: \(\widehat{DBC}+\widehat{ABC}=\widehat{ABD}\)(tia BC nằm giữa hai tia BA,BD)
nên \(\widehat{DBC}+\widehat{ABC}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{KBC}=\widehat{DBC}\)
hay BC là tia phân giác của \(\widehat{KBD}\)(đpcm)