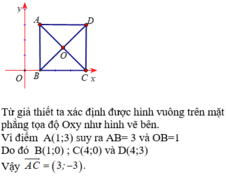
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
♬ დ დ MINIGAME NHANH NHƯ CHỚP SỐ THỨ 7 NGÀY 16/2/2019♬ დ დ Ⓐ Ⓛ Ⓕ Ⓐ Ⓩ Ⓘ —->Ra mắt Shop Quà tặng Alfazi: https://alfazi.edu.vn/question/5b7cb22b658d8953adc4773c Ⓐ Ⓛ Ⓕ Ⓐ Ⓩ Ⓘ —->Mua hàng tại Shop Quà tặng Alfazi: https://alfazi.edu.vn/question/5b7cb44b658d8953adc47748 Ⓐ Ⓛ Ⓕ Ⓐ Ⓩ Ⓘ LINK MỜI BẠN BÈ THAM GIA SỐ THỨ 7 NHANH NHƯ CHỚP: https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b (Copy gửi cho các bạn của mình nhé!) ❁ ✪ 1. Thời gian: Bắt đầu từ lúc 6h hoặc 8h Kết thúc lúc 21h ngày hôm sau. Thời gian công bố kết quả: 21h30 phút ngày hôm sau. ❁ ✪ 2. CÂU HỎI NGÀY HÔM NAY: “Bạn làm việc gì đầu tiên mỗi buổi sáng?” 👌🏻Giải thích câu trả lời! ❁ ✪ 3.Hình thức: Khi các bạn tham gia MiniGame Nhanh Như Chớp, các bạn sẽ nhận được ĐIỂM. ĐIỂM sẽ được tích luỹ từ số này qua số khác của Minigame. Các bạn hãy tích luỹ ĐIỂM để mua hàng tại Shop: ❁ ✪ -Tham gia trả lời câu hỏi:+1 điểm ❁ ✪ -Mỗi câu trả lời đúng: +1 điểm ❁ ✪ -Mời một bạn cùng tham gia: +1 điểm/1 bạn ❁ ✪ Các bạn hãy comment theo mẫu: “Câu trả lời+tên 3 bạn mà bạn đã mời” ——>Chỉ những bình luận làm theo mẫu mới được tính❤️❤️ ❁ ✪ LINK MỜI BẠN BÈ THAM GIA SỐ THỨ 7 NHANH NHƯ CHỚP: https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b (Copy gửi cho các bạn của mình nhé!) ❁ ✪ ĐIỂM SẼ ĐƯỢC TÍCH LUỸ TỪ SỐ NÀY QUA SỐ KHÁC CỦA MINIGAME NHANH NHƯ CHỚP NÊN CƠ HỘI RẤT NHIỀU CÁC BẠN NHÉ! ❁ ✪ Các bạn sẽ thắc mắc điểm dùng để làm gì? ❁ ✪ ĐIỂM sẽ dùng để mua hàng tại Shop Alfazi. ❁ ✪ —->Ra mắt Shop Quà tặng Alfazi: https://alfazi.edu.vn/question/5b7cb22b658d8953adc4773c ❁ ✪ —->Mua hàng tại Shop Quà tặng Alfazi: https://alfazi.edu.vn/question/5b7cb44b658d8953adc47748 ❁ ✪ LINK MỜI BẠN BÈ THAM GIA SỐ THỨ 7 NHANH NHƯ CHỚP: https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b (Copy gửi cho các bạn của mình nhé!) Thân, Nhóm phát triển cộng đồng❤️❤️
Câu 1 đề thiếu, điểm C thỏa mãn điều gì nữa? (ví dụ G là trọng tâm tam giác?)
Câu 2:
Do B, C đều thuộc d nên tọa độ có dạng: \(B\left(2b-3;b\right);C\left(2c-3;c\right)\) với \(b\ne c\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2c-2;c-2\right)\\\overrightarrow{BC}=\left(2c-2b;c-b\right)\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{BC}=0\\AC=3BC\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(2c-2\right)\left(2c-2b\right)+\left(c-2\right)\left(c-b\right)=0\\\left(2c-2\right)^2+\left(c-2\right)^2=9\left(2c-2b\right)^2+9\left(c-b\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4c-4+c-2=0\\\left(2c-2\right)^2+\left(c-2\right)^2=45\left(c-b\right)^2\end{matrix}\right.\)
\(\Rightarrow...\)
Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong
a: A(2;1); B(-2;5); C(-5;2)
Tọa độ vecto AB là:
\(\left\{{}\begin{matrix}x=-2-2=-4\\y=5-1=4\end{matrix}\right.\)
Vậy: \(\overrightarrow{AB}=\left(-4;4\right)\)
Tọa độ vecto AC là:
\(\left\{{}\begin{matrix}x=-5-2=-7\\y=2-1=1\end{matrix}\right.\)
Vậy: \(\overrightarrow{AC}=\left(-7;1\right)\)
Tọa độ vecto BC là:
\(\left\{{}\begin{matrix}x=-5-\left(-2\right)=-5+2=-3\\y=2-5=-3\end{matrix}\right.\)
Vậy: \(\overrightarrow{BC}=\left(-3;-3\right)\)
b: \(\overrightarrow{AB}=\left(-4;4\right);\overrightarrow{AC}=\left(-7;1\right);\overrightarrow{BC}=\left(-3;-3\right)\)
\(AB=\sqrt{\left(-4\right)^2+4^2}=4\sqrt{2}\)
\(AC=\sqrt{\left(-7\right)^2+1^2}=5\sqrt{2}\)
\(BC=\sqrt{\left(-3\right)^2+\left(-3\right)^2}=3\sqrt{2}\)
Chu vi ΔABC là:
\(5\sqrt{2}+4\sqrt{2}+3\sqrt{2}=12\sqrt{2}\)
Vì \(AC^2=BA^2+BC^2\)
nên ΔABC vuông tại B
c: tọa độ I là:
\(\left\{{}\begin{matrix}x=\dfrac{2+\left(-2\right)}{2}=0\\y=\dfrac{1+5}{2}=\dfrac{6}{2}=3\end{matrix}\right.\)
Vậy: I(0;3)
d: Tọa độ trọng tâm G của ΔABC là:
\(\left\{{}\begin{matrix}x=\dfrac{2+\left(-2\right)+\left(-5\right)}{3}=-\dfrac{5}{3}\\y=\dfrac{1+5+2}{3}=\dfrac{8}{3}\end{matrix}\right.\)
e: ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
mà \(\overrightarrow{AB}=\left(-4;4\right);\overrightarrow{DC}=\left(-5-x;2-y\right)\)
nên \(\left\{{}\begin{matrix}-5-x=-4\\2-y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5=4\\y=2-4=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Vậy: D(-1;-2)
a: vecto AB=(-3;-4)
vecto AC=(3;-2)
Vì -3/3<>-4/2-2
nên A,B,C là ba đỉnh của 1 tam giác
b: Tọa độ G là:
x=(2-1+5)/3=2 và y=(3-1+1)/3=2
=>G(2;2) và A(2;3)
Tọa độ I là:
x=(2+2)/2=2 và y=(2+3)/2=2,5
c: K thuộc Oy nên K(0;y)
vecto AI=(0;-0,5); vecto AK=(-2;y-3)
Theo đề, ta có:
0/-2=-0,5/y-3
=>-0,5/y-3=0
=>Ko có K thỏa mãn