Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

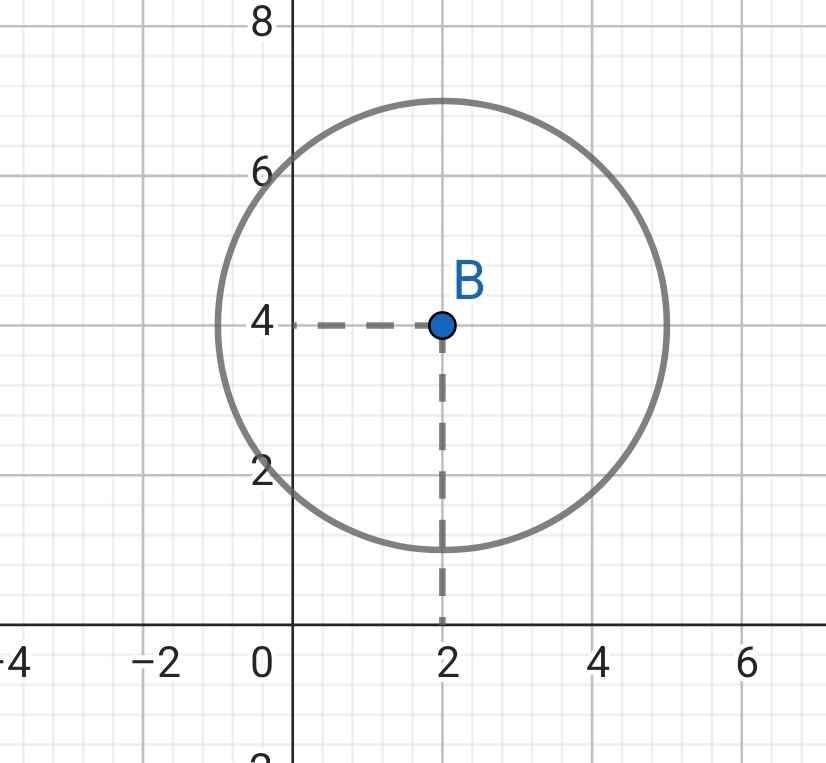 Do 3 < 4 nên (B; 3 cm) và Ox không giao nhau
Do 3 < 4 nên (B; 3 cm) và Ox không giao nhau
Do 3 > 2 nên (B; 3 cm) và Oy cắt nhau tại 2 điểm

Để xác định vị trí tương đối của một điểm và một đường tròn chỉ cần tính khoảng cách từ điểm đó tới tâm của đường tròn.
c) Gọi I là trung điểm BC, R là bán kính đường tròn
=> \(HI=\frac{1}{2}AH=\frac{1}{2}.R\)
Ta có: K là điểm đối xứng với H qua BC
=> \(KH=2.HI=2.\frac{1}{2}R=R\)
=> K thuộc đường tròn
( Chú ý nếu trong trường hợp: tính được KH < R => K nằm trong đường tròn và KH>R thì K nằm ngoài đường tròn)

Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy

`y=ax-2` `(1)` `(a \ne 0)`
H/s `(1)` cắt trục hoành `Ox=>y=0`
`=>0=ax-2<=>x=2/a`
Mà h/s `(1)` cắt `Ox` tại `A`
`=>x=OA=2/a` `(2)`
H/s `(1)` cắt trục tung `Oy=>x=0`
`=>y=a.0-2<=>y=-2`
Mà h/s `(1)` cắt `Oy` tại `B`
`=>y=OB=-2` `(3)`
Có: `OB=2OA` `(4)`
Từ `(2);(3);(4)=>-2=2. 2/a`
`<=>-2a=4<=>a=-2` (t/m `a \ne 0`)
`=>` Đths `(1)` có dạng: `y=-2x-2`
Bạn thử xem lại đề chứ `a < 0` á .-.

Gọi R là bán kính của đường tròn (O; 2). Ta có: R = 2
O A 2 = 1 2 + 1 2 = 2 ⇒ OA = 2 < 2
Vì OA < R nên điểm A nằm trong đường tròn (O; 2)
O B 2 = 2 2 + 2 2 = 2 + 2 = 4 ⇒ OB = 2
Vì OB = R nên điểm B thuộc đường tròn (O; 2)
O C 2 = 1 2 + 2 2 = 1 + 4 = 5 ⇒ OC = 5 > 2

a: Đặt (d1): y=ax+b(a<>0)
Vì (d1) vuông góc với (d) nên 3a=-1
=>\(a=-\dfrac{1}{3}\)
Vậy: (d1): \(y=-\dfrac{1}{3}x+b\)
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x=-b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{x}{3}=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3b\\y=0\end{matrix}\right.\)
=>A(3b;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{3}\cdot0+b=b\end{matrix}\right.\)
=>B(0;b)
\(AB=2\sqrt{10}\)
=>\(AB^2=40\)
=>\(\left(0-3b\right)^2+\left(b-0\right)^2=40\)
=>\(10b^2=40\)
=>\(b^2=4\)
=>b=2 hoặc b=-2
Vậy: (d1): y=-1/3x+2 hoặc (d1): y=-1/3x-2
b: Đặt (d2): y=ax+b
Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-5\end{matrix}\right.\)
Vậy: (d2): y=3x+b
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\3x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{b}{3}\end{matrix}\right.\)
=>\(C\left(-\dfrac{b}{3};0\right)\)
tọa độ D là:
\(\left\{{}\begin{matrix}x=0\\y=3x+b=3\cdot0+b=b\end{matrix}\right.\)
=>D(0;b)
\(OC=\sqrt{\left(-\dfrac{b}{3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{b}{3}\right)^2+0}=\dfrac{\left|b\right|}{3}\)
\(OD=\sqrt{\left(0-0\right)^2+\left(b-0\right)^2}=\sqrt{0^2+b^2}=\left|b\right|\)
Vì Ox\(\perp\)Oy nên OC\(\perp\)OD
=>ΔOCD vuông tại O
=>\(S_{OCD}=\dfrac{1}{2}\cdot OC\cdot OD\)
=>\(S_{OCD}=\dfrac{\dfrac{1}{2}\left|b\right|}{3}\cdot\left|b\right|=\dfrac{1}{2}\cdot\dfrac{b^2}{3}\)
Để \(S_{OCD}=6\) thì \(\dfrac{b^2}{6}=6\)
=>\(b^2=36\)
=>\(b=\pm6\)
Vậy: (d2): y=3x+6 hoặc (d2): y=3x-6
Để ΔOCD cân tại O thì OC=OD
=>\(\dfrac{\left|b\right|}{3}=\left|b\right|\)
=>\(\left|b\right|=0\)
=>b=0
Vậy: (d2): y=3x

a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2

Sửa đề: (d); y=(k-1)x+2k
a: Để (d)//Ox thì k-1=0
=>k=2
b: Thya x=-3 và y=5 vào (d),ta được:
-3(k-1)+2k=5
=>-3k+3+2k=5
=>3-k=5
=>k=-2
c: Tọa độ A là:
y=0 và (k-1)x+2k=0
=>x=-2k/k-1 và y=0
=>OA=2|k/k-1|
Tọa độ B là:
x=0 và y=(k-1)*0+2k=2k
=>OB=|2k|
Theo đề, ta có: \(\dfrac{1}{2}\cdot OA\cdot OB=1\)
=>\(\dfrac{2\left|k\right|\cdot\left|k\right|}{\left|k-1\right|}=1\)
=>2k^2=|k-1|
TH1: k>1
=>2k^2=k-1
=>2k^2-k+1=0
=>Loại
TH2: k<1
=>2k^2=-k+1
=>2k^2+k-1=0
=>2k^2+2k-k-1=0
=>(k+1)(2k-1)=0
=>k=1/2(nhận) hoặc k=-1(nhận)

(A;1) có R=1
A(1;2) có hoành độ là 1=R và tung độ là 2>R
nên (A;1) sẽ tiếp xúc với trục Ox và sẽ không giao với trục Oy
(A;2) có R=2
A(1;2) có hoành độ là 1<R và tung độ là 2=R
=>(A;2) sẽ cắt trục Ox và tiếp xúc với trục Oy
e cảm ơn ạ