Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(A=\dfrac{a^{\dfrac{4}{3}}\left(a^{-\dfrac{1}{3}}+a^{\dfrac{2}{3}}\right)}{a^{\dfrac{1}{4}}\left(a^{\dfrac{3}{4}}+a^{-\dfrac{1}{4}}\right)}=\dfrac{a^{\left(\dfrac{4}{3}-\dfrac{1}{3}\right)+}a^{\left(\dfrac{4}{3}+\dfrac{2}{3}\right)}}{a^{\left(\dfrac{1}{4}+\dfrac{3}{4}\right)}+a^{\left(\dfrac{1}{4}-\dfrac{1}{4}\right)}}=\dfrac{a+a^2}{a+1}=\dfrac{a\left(a+1\right)}{a+1}\)
\(a>0\Rightarrow a+1\ne0\) \(\Rightarrow A=a\)

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

a 1 3 b + b 1 3 a a 6 + b 6 = a 1 3 b 1 2 + b 1 3 a 1 2 a 1 6 + b 1 6
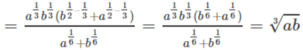

Câu a, b thì Nguyễn Quang Duy làm đúng rồi.
c) \(a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\)
d) \(\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}\)

\(=\left[\frac{\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)\left(a+a^{\frac{1}{2}}b^{\frac{1}{2}}+b\right)}{a^{\frac{1}{2}}-b^{\frac{1}{2}}}+a^{\frac{1}{2}}b^{\frac{1}{2}}\right]\left[\frac{a^{\frac{1}{2}}-b^{\frac{1}{2}}}{\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)}\right]^2\)
\(=\frac{a+2a^{\frac{1}{2}}b^{\frac{1}{2}}+b}{\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)^2}=\frac{\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)^2}{\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)^2}=1\)

\(A=\log_a\left(a^2\sqrt[4]{a^3\sqrt[5]{a}}\right)=\log_a\left(a^2\sqrt[4]{a^3.a^{\frac{1}{5}}}\right)=\log_a\left[a^2\left(a^{\frac{16}{5}}\right)^{\frac{1}{4}}\right]=\log_a\left(a^2.a^{\frac{4}{5}}\right)=\frac{14}{5}\)
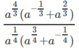
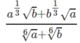
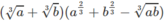
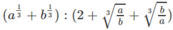
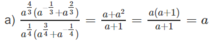
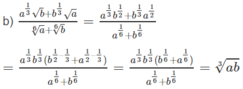
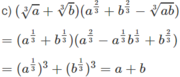
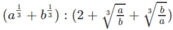
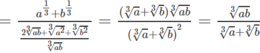
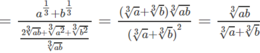
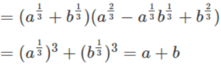
a 4 3 a - 1 3 + a 2 3 a 1 4 a 3 4 + a - 1 4 = a + a 2 a + 1 = a a + 1 a + 1 = a