Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

DI//CF
=>góc EID=góc EFC=góc EBD
=>EBID nội tiếp
=>góc EDB=góc EIB
mà góc EIB=góc KOB
nên góc EDB=góc KOB
=>góc KDB=góc KOB
=>KBOD nộitiếp

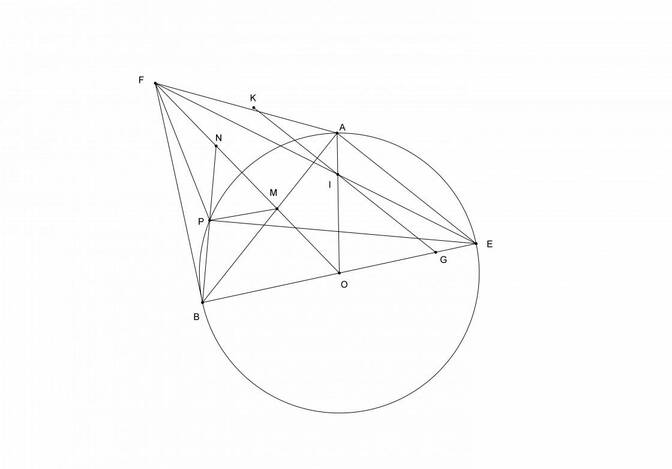
a. Tứ giác AOBF nội tiếp vì có $\angle OAF=\angle OBF=90^o$
b. Chú ý rằng $OF\perp AB$ nên $OF\parallel AE$, ta biến đổi tỉ số bằng định lý Thales:
\(\dfrac{IK}{OF}=\dfrac{AK}{AF}=\dfrac{EG}{EO}=\dfrac{IG}{OF}\), vậy $IK=IG$
c. Nếu mình không nhầm thì PM không vuông NB, vì khi đó $M,P,E$ thẳng hàng, bạn có thể kiểm tra hình vẽ của mình :c

a/
Ta có A và B cùng nhìn FO dưới 1 góc vuông => A và B thuộc đường tròn đường kính FO
=> AOBF là tứ giác nội tiếp
b/
Ta có
\(\widehat{BAE}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow AE\perp AB\) (1)
\(FO\perp AB\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn vuông góc và chia đôi dây cung nối 2 tiếp điểm) (2)
Từ (1) và (2) => AE//FO mà KG//AE (gt) => AE//KG//FO
\(\Rightarrow\dfrac{FK}{FA}=\dfrac{OG}{OE}\) (Talet) (1)
Xét tg AFE có
\(\dfrac{FK}{FA}=\dfrac{IK}{AE}\) (Talet trong tam giác) (2)
Xét tg OAE có
\(\dfrac{OG}{OE}=\dfrac{IG}{AE}\) (Talet trong tam giác) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{IK}{AE}=\dfrac{IG}{AE}\Rightarrow IK=IG\)
c/ Câu này mình nghĩ bạn nên kiểm tra lại đề bài

4]
tg DEC ~ tg DCB
=> EC/BC = DC/DB
=> EC = BC.DC/DB
=> AC.EC = AC.BC.DC/DB = 2S(ACB).DC/DB
Cần c/m AF.CH = AC.EC
<=> AF.CH = 2S(ACB).DC/DB
<=> AE.DB = 2S(ACB).DC/CH (*)
Mà 2S(ACB)/CH = AB
=> (*) <=> AE.DB = AB.DC = AB.DA
Mà AE.DB = 2S(ADB); AB.DA = 2S(ADB)
Vậy: AF.CH = AC.EC
5]
Ta đi c/m KA=KD để suy ra KE là tiếp tuyến.
AE kéo dài CH tại M
=> AK/CM = KI/IC
=> KD/CH = KI/IC
=> AK/CM = KD/CH (*)
DP cắt CH tại P; BC cắt AD tại J
=> HP/AD = BP/BD = CP/DJ (**)
Tam giác ACJ vuông tại C, AD=AD => DC là trung tuyến => AD=DJ
Từ (**) => HP=PC
Xét 2 tg vuông AMH và HBP, ta có ^AMH = ^HBP (cạnh tương ứng vuông góc)
=> tg AMH ~ HBP
=> MH/AH = HB/PH
=> MH = AH.HB/PH = AH.HB/(CH/2) = 2AH.HB/CH (***)
Do CH^2 = AH.HB => AH.HB/CH = CH
Từ (***) => MH = 2CH => CM =CH
Từ (*) => AK =KD
=> KE là trung tuyến tg vuông ADE => ka=ke
=> tg OKA = tg OKE (do OA=OE, OK chung; AK=KD)
=> ^KEO = ^KAO = 90
=> KE là tiếp tuyến của (O)

a: Sửa đề: AEBF là hình chữ nhật
Xét tứ giác AEBF có
AB cắt EF tại trung điểm của mỗi đường
nên AEBF là hình bình hành
Hình bình hành AEBF có AB=EF
nên AEBF là hình chữ nhật
b: ΔBEH vuông tại E
mà EP là đường trung tuyến
nên EP=PB=PH=HB/2
Xét ΔOBP và ΔOEP có
OB=OE
BP=EP
OP chung
Do đó: ΔOBP=ΔOEP
=>\(\widehat{OEP}=\widehat{OBP}=90^0\)
=>PE là tiếp tuyến của (O)
c: AM\(\perp\)EF
=>\(\widehat{AFE}+\widehat{MAK}=90^0\)
mà \(\widehat{AFE}=\widehat{ABE}\)(AFBE là hình chữ nhật)
nên \(\widehat{MAK}+\widehat{ABE}=90^0\)
mà \(\widehat{ABE}=\widehat{AHK}\left(=90^0-\widehat{BAH}\right)\)
nên \(\widehat{MAK}+\widehat{AHK}=90^0\)
mà \(\widehat{MKA}+\widehat{AHK}=90^0\)(ΔAKH vuông tại A)
nên \(\widehat{MAK}=\widehat{MKA}\)
=>MA=MK
\(\widehat{MAK}+\widehat{MAH}=90^0\)
\(\widehat{MKA}+\widehat{MHA}=90^0\)
mà \(\widehat{MAK}=\widehat{MKA}\)
nên \(\widehat{MAH}=\widehat{MHA}\)
=>MA=MH
mà MA=MK
nên MK=MH
=>M là trung điểm của KH




bài này khó hơn
de om chung minh thoi chu gi
* vi diem i nam giua 2 diem con lai
* vi diem i cach deu 2 diem h va k