CL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
14 tháng 9
Câu 25. Hai đoạn \(A = \left[\right. a ; a + 2 \left]\right.\), \(B = \left[\right. b ; b + 1 \left]\right.\), tìm số \(a - b\) nguyên để \(A \cap B = \emptyset\)
Điều kiện \(A \cap B = \emptyset\) nghĩa là:
\(a + 2 < b \text{ho}ặ\text{c} b + 1 < a\)
- Trường hợp 1: \(a + 2 < b \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } b - a > 2 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } a - b < - 2\)
- Trường hợp 2: \(b + 1 < a \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } a - b > 1\)
Vậy \(a - b\) nguyên thỏa:
\(a - b < - 2 \text{ho}ặ\text{c} a - b > 1\)
- Số nguyên thỏa: \(. . . , - 3 , - 4 , - 5 , . . .\) và \(2 , 3 , 4 , . . .\)
- Kết luận: Có vô số số nguyên \(a - b\), nhưng nếu yêu cầu liệt kê, thì tất cả số nguyên \(a - b \leq - 3\) hoặc \(a - b \geq 2\).
Câu 26. Ba tập hợp:
\(A = \left(\right. - 3 , - 1 \left.\right) \cup \left(\right. 1 , 2 \left.\right) , B = \left(\right. m - 1 , + \infty \left.\right) , C = \left(\right. - \infty , 2 m + 1 \left.\right)\)
Điều kiện \(A \cap B \cap C = \emptyset\) nghĩa là không có phần tử chung.
- Giao ba tập: \(\left(\right. A \cap B \left.\right) \cap C = \emptyset\)
Bước 1: Giao \(A\) và \(B\)
- \(A_{1} = \left(\right. - 3 , - 1 \left.\right)\), \(A_{2} = \left(\right. 1 , 2 \left.\right)\)
- \(B = \left(\right. m - 1 , + \infty \left.\right)\)
Giao không rỗng nếu:
- \(A_{1} \cap B \neq \emptyset \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } m - 1 < - 1 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } m < 0\)
- \(A_{2} \cap B \neq \emptyset \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } m - 1 < 2 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } m < 3\)
Bước 2: Giao với \(C = \left(\right. - \infty , 2 m + 1 \left.\right)\)
- Nếu muốn \(A \cap B \cap C = \emptyset\), phải chọn \(m\) để giao này rỗng.
- Phân tích từng khoảng, ta tìm được m < 0 hoặc m > ??? (phải tính chi tiết)
Với các câu tiếp theo (27–35), cách giải chung là:
- Viết lại điều kiện giao, hợp, phần tử nguyên.
- Tìm nghiệm của tham số sao cho điều kiện đúng.
- Kiểm tra số phần tử hoặc tổng theo yêu cầu.
14 tháng 9
Câu 33: Để a nguyên thì 3b-8⋮b+2
=>3b+6-14⋮b+2
=>-14⋮b+2
=>b+2∈{1;-1;2;-2;7;-7;14;-14}
=>b∈{-1;-3;0;-4;5;-9;12;-16}
=>A có 8 phần tử
Câu 32:
Để B khác rỗng thì 2a<3a+1
=>-a<1
=>a>-1
Để A giao B=rỗng thì 2a>=5 hoặc 3a+1<0
=>a>=5/2 hoặc a<-1/3
=>a>=5/2 hoặc -1<a<-1/3
mà a nguyên
nên a>=5/2
=>Có vô số giá trị a nguyên để A giao B=rỗng
CM
22 tháng 4 2019
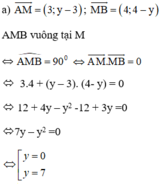
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.
Vậy P(-5; 2)
NN
0
24 tháng 8 2021
a)\(\left(-3;m\right)\subset\)\((-4;5]\)
\(\Leftrightarrow m\le5\)
b)\(\left(m+1;3+m\right)\cap\)\([-3;5)\)\(=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}3+m< -3\\m+1\ge5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m< -6\\m\ge4\end{matrix}\right.\)
Vậy..
11 tháng 3 2023
a: vecto AB=(2-m;-2)
vecto AC=(-4-m;2)
Để A,B,C ko thẳng hàng thì \(\dfrac{2-m}{-4-m}< >\dfrac{-2}{2}=-1\)
=>2-m<>m+4
=>-2m<>2
=>m<>-1
b: Tọa độ trọng tâm là:
\(\left\{{}\begin{matrix}x=\dfrac{m+2-4}{3}=\dfrac{m-2}{3}\\y=\dfrac{3+1+5}{3}=3\end{matrix}\right.\)
Để M nằm trên d thì \(\left\{{}\begin{matrix}\dfrac{m-2}{3}=t+1\\5-2t=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t=1\\m-2=3\cdot2=6\end{matrix}\right.\Leftrightarrow m=8\)
11 tháng 3 2023
a: vecto AB=(2-m;-2)
vecto AC=(-4-m;2)
Để A,B,C ko thẳng hàng thì \(\dfrac{2-m}{-4-m}< >\dfrac{-2}{2}=-1\)
=>2-m<>m+4
=>-2m<>2
=>m<>-1
b: Tọa độ trọng tâm là:
\(\left\{{}\begin{matrix}x=\dfrac{m+2-4}{3}=\dfrac{m-2}{3}\\y=\dfrac{3+1+5}{3}=3\end{matrix}\right.\)
Để M nằm trên d thì \(\left\{{}\begin{matrix}\dfrac{m-2}{3}=t+1\\5-2t=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t=1\\m-2=3\cdot2=6\end{matrix}\right.\Leftrightarrow m=8\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2021
a.
\(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}m+4< -5\\m>11\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -9\\m>11\end{matrix}\right.\)
b.
\(A\cap B\ne\varnothing\Leftrightarrow-9\le m\le11\)