Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\left(\frac{\sqrt{a}+1}{\sqrt{a}-1}-\frac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}+\frac{1}{\sqrt{a}}\right)\)
\(A=\)\(\left[\frac{\left(\sqrt{a}+1\right)^2-\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}+\frac{4\sqrt{a}\left(a-1\right)}{a-1}\right]\left[\frac{a+1}{\sqrt{a}}\right]\)
\(A=\frac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4a\sqrt{a}-4\sqrt{a}}{a-1}.\) \(\frac{a+1}{\sqrt{a}}\)
\(A=\frac{4a\sqrt{a}}{a-1}.\frac{a+1}{\sqrt{a}}\)
\(A=\frac{4a\left(a+1\right)}{a-1}\)
ta có \(a=\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}\)
\(a=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\)
\(a=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(a=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(a=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(a=\left(4+\sqrt{15}\right).2\left(4-\sqrt{15}\right)\)
\(a=2\left(16-15\right)\)
\(a=2\)
khi đó \(A=\frac{4.2.\left(2+1\right)}{2-1}=8.3=24\)
vậy.....

a)A=(\(\frac{2}{\sqrt{a}-1}\)+\(\frac{2}{\sqrt{a}+1}\)+4\(\sqrt{a}\)).\(\frac{a-1}{\sqrt{a}}\)=(\(\frac{4\sqrt{a}}{a-1}\)+4\(\sqrt{a}\)).\(\frac{a-1}{\sqrt{a}}\)=\(\frac{4a}{a-1}\)
b)a=(\(\sqrt{\left(4+\sqrt{15}\right).\left(4-\sqrt{15}\right)}\).(\(\sqrt{10}\)-\(\sqrt{6}\))=\(\sqrt{16-15}\).(\(\sqrt{10}\)-\(\sqrt{6}\))=\(\sqrt{10}\)-\(\sqrt{6}\)
Thay vào A rồi tính là xong
a) \(A=\left(\frac{\sqrt{a}+1}{\sqrt{a}-1}-\frac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}-\frac{1}{\sqrt{a}}\right)\)
\(=\left[\frac{\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\frac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}+4\sqrt{a}\right].\left(\frac{a}{\sqrt{a}}-\frac{1}{\sqrt{a}}\right)\)
\(=\left[\frac{a+2\sqrt{a}+1}{a-1}-\frac{a-2\sqrt{a}+1}{a-1}+\frac{4\sqrt{a}\left(a-1\right)}{a-1}\right].\frac{a-1}{\sqrt{a}}\)
\(=\frac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4\sqrt{a}.a-4\sqrt{a}}{a-1}.\frac{a-1}{\sqrt{a}}\)
\(=\frac{4\sqrt{a}.a}{a-1}.\frac{a-1}{\sqrt{a}}=4a\)
b) Ta có: \(a=\left(\sqrt{4+\sqrt{15}}\right)\left(\sqrt{10}-\sqrt{6}\right)\left(\sqrt{4-\sqrt{15}}\right)\)
\(=\left(\sqrt{4+\sqrt{15}}\right)\left(\sqrt{4-\sqrt{15}}\right)\left(\sqrt{10}-\sqrt{6}\right)\)
\(=\sqrt{\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)}.\left(\sqrt{10}-\sqrt{6}\right)\)
\(=\sqrt{16-15}.\left(\sqrt{10}-\sqrt{6}\right)=\sqrt{10}-\sqrt{6}\)
Thay a vào A ta được: \(A=4.\left(\sqrt{10}-\sqrt{6}\right)=4\sqrt{10}-4\sqrt{6}\)

\(\begin{array}{l} a)A = \left( {\dfrac{{\sqrt a + 1}}{{\sqrt a - 1}} - \dfrac{{\sqrt a - 1}}{{\sqrt a + 1}} + 4\sqrt a } \right).\left( {\sqrt a + \dfrac{1}{{\sqrt a }}} \right)\\ = \left[ {\dfrac{{{{\left( {\sqrt a + 1} \right)}^2} - {{\left( {\sqrt a - 1} \right)}^2}}}{{\left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}} + 4\sqrt a } \right].\dfrac{{a + 1}}{{\sqrt a }}\\ = \left[ {\dfrac{{4\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}} + 4\sqrt a } \right].\dfrac{{a + 1}}{{\sqrt a }}\\ = \dfrac{{4\sqrt a + 4\sqrt a \left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}}{{\left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}}.\dfrac{{a + 1}}{{\sqrt a }}\\ = \dfrac{{4a\sqrt a }}{{a - 1}}.\dfrac{{a + 1}}{{\sqrt a }} = \dfrac{{4a}}{{a - 1}}\left( {a + 1} \right) = \dfrac{{4{a^2} + 4a}}{{a - 1}} \end{array}\)
$b)$Thay $a=\left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right)$ vào ta được:
$A=\dfrac{4{{\left[ \left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right) \right]}^{2}}+4\left[ \left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right) \right]}{\left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right)-1}=12$
$\begin{align}
& a)A=\left( \dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a} \right).\left( \sqrt{a}+\dfrac{1}{\sqrt{a}} \right) \\
& =\left[ \dfrac{{{\left( \sqrt{a}+1 \right)}^{2}}-{{\left( \sqrt{a}-1 \right)}^{2}}}{\left( \sqrt{a}-1 \right)\left( \sqrt{a}+1 \right)}+4\sqrt{a} \right].\dfrac{a+1}{\sqrt{a}} \\
& =\left[ \dfrac{4\sqrt{a}}{\left( \sqrt{a}-1 \right)\left( \sqrt{a}+1 \right)}+4\sqrt{a} \right].\dfrac{a+1}{\sqrt{a}} \\
& =\dfrac{4\sqrt{a}+4\sqrt{a}\left( \sqrt{a}-1 \right)\left( \sqrt{a}+1 \right)}{\left( \sqrt{a}-1 \right)\left( \sqrt{a}+1 \right)}.\dfrac{a+1}{\sqrt{a}} \\
& =\dfrac{4a\sqrt{a}}{a-1}.\dfrac{a+1}{\sqrt{a}}=\dfrac{4a}{a-1}\left( a+1 \right)=\dfrac{4{{a}^{2}}+4a}{a-1} \\
\end{align}$
$b)$Thay $a=\left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right)$ vào ta được:
$A=\dfrac{4{{\left[ \left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right) \right]}^{2}}+4\left[ \left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right) \right]}{\left( 4+\sqrt{15} \right)\left( \sqrt{10}-\sqrt{6} \right)\left( \sqrt{4-\sqrt{15}} \right)-1}=12$

Bài 1:
a: \(=\sqrt{\dfrac{7-4\sqrt{3}}{2-\sqrt{3}}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Bài 2:
\(VT=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)

a, A\(=\left(\frac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2+4\sqrt{x}\left(x-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right):\frac{x-1}{\sqrt{x}}\) ĐK x>0 ;\(x\ne1;x\ne-1\)
\(A=\frac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4x\sqrt{x}-4\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\frac{\sqrt{x}}{x-1}\)
\(A=\frac{4x\sqrt{x}}{x-1}.\frac{\sqrt{x}}{x-1}\)=\(\frac{4x^2}{\left(x-1\right)^2}\)
b, Để A =2 \(\Rightarrow\frac{4x^2}{\left(x-1\right)^2}=2\Rightarrow4x^2=2\left(x-1\right)^2\)
<=> \(4x^2=2x^2-4x+2\)
<=> \(2x^2+4x-2=0\)
<=> \(x^2+2x-1=0\)
\(\Delta=1^2-1.\left(-1\right)\) = 2
=> \(\orbr{\begin{cases}x_1=-1-\sqrt{2}\left(loại\right)\\x_2=-1+\sqrt{2}\left(nhận\right)\end{cases}}\)
Vậy x=\(-1+\sqrt{2}\)thì A =2
c, Thay x =\(\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}\)=2
=>A = \(\frac{4.2^2}{\left(2-1\right)^2}=16\)
Vậy A=16 thì x=\(\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}\)

1) \(A^2=2+2.\frac{\sqrt{\left(8+\sqrt{15}\right)\left(8-\sqrt{15}\right)}}{2}\)
\(2+\sqrt{64-15}=2+\sqrt{49}=2+7=9\) mà A>0
=> A=3
2) \(A=\sqrt{4-\sqrt{15}}\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right).\)
\(A=\sqrt{\left(4-\sqrt{15}\right)\left(4+\sqrt{15}\right)}\sqrt{4+\sqrt{15}}\left(\sqrt{10}-\sqrt{6}\right).\)
\(A=\sqrt{4+\sqrt{15}}\left(\sqrt{10}-\sqrt{6}\right).\)
\(A^2=\left(4+\sqrt{15}\right)\left(16-4\sqrt{15}\right)\)
\(=4\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)=4\)
Mà A >0
=> A=2
Mà 4>3
=> \(\sqrt{4}=2>\sqrt{3}\)
=> \(A>\sqrt{3}\)
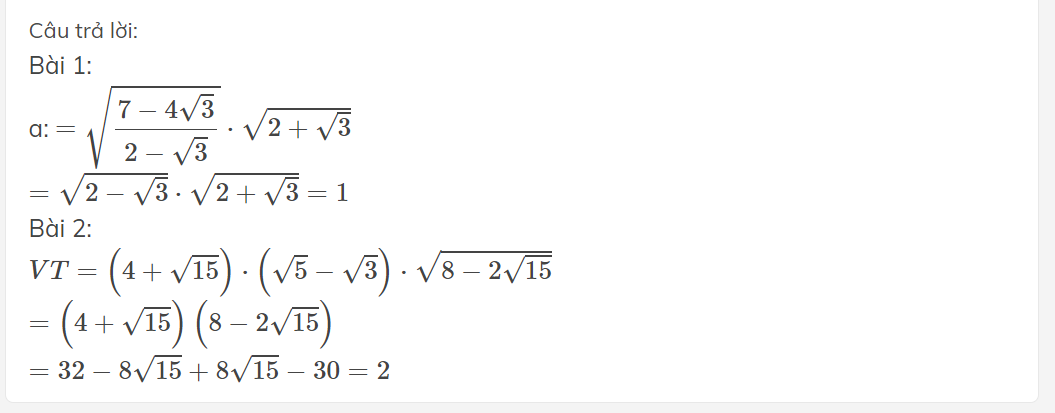
ở \(\sqrt{\left(25-\sqrt{15}\right)^2}\) sửa thành \(\sqrt{\left(5-\sqrt{15}\right)^2}\)