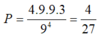Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số phần tử của E là ![]() Trong E có 6 số chia hết cho 10 là 10, 20, 30, 40, 50, 60.
Trong E có 6 số chia hết cho 10 là 10, 20, 30, 40, 50, 60.
Số cách lấy ngẫu nhiên đồng thời hai phần tử trong E là ![]() cặp.
cặp.
Biến cố M “lấy được ít nhất một số chia hết cho 10” gồm ![]() cách lấy được 2 số chia hết cho 10 và
cách lấy được 2 số chia hết cho 10 và ![]() cách lấy được 1 số chia hết cho 10 và 1 số không chia hết cho 10.
cách lấy được 1 số chia hết cho 10 và 1 số không chia hết cho 10.
Vậy số phần tử của biến cố M là
![]()

Số các số có `8` chữ số đôi một khác nhau là `9.A_9^7`(số)
`=> n(A) = n(\Omega) = 9.A_9^7`
Dễ thấy rằng `0 + 1 + 2 + .. + 9 = 45 \vdots 9`
Gọi `X = {0;1;..;9}`
Để số đó chia hết cho `8` thì nó phải được chọn từ các tập
`X \\ {0;9}` , `X \\ {1;8}` , `X \\ {2;7}` , `X \\ {3;6}` , `X \\ {4;5}`
Ta xét `2` trường hợp như sau:
Trường hợp `1`: Số đó được chọn từ tập `X \\ {0;9}`
Xếp `8` số vào `8` vị trí có `8!`(cách)
Trường hợp `2`:Số đó được chọn từ `4` tập còn lại
Chọn `1` trong `4` tập có `C_4^1`(cách)
Xếp `8` chữ số vừa chọn `1` cách ngẫu nhiên có `8!`(cách)
Cho số `0` đứng đầu xếp `7` số còn lại có `7!` cách
Số lập được:`4(8!-7!)`(số)
Gọi `B` là biến cố chọn được số chia hết cho `9` từ tập `A`
`=> |B| = 8! + 4(8!-7!)`
Xác xuất biến cố `B`:
`P(B) = \frac{8!+4(8!-7!)}{9.A_9^7} = \frac{1}{9}`

"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?

Có 900 số tự nhiên có 3 chữ số \( \Rightarrow n\left( \Omega \right) = 900\)
Gọi \({A_1}\) là biến cố: “Số được chọn chia hết cho 2”, \({A_2}\) là biến cố “Số được chọn chia hết cho 7”.
Vậy \({A_1}{A_2}\) là biến cố “Số được chọn chia hết cho 14”, \(A = {A_1} \cup {A_2}\) là biến cố “Số được chọn chia hết cho 2 hoặc 7”.
Có 450 số có 3 chữ số chia hết cho 2 \( \Rightarrow n\left( {{A_1}} \right) = 450 \Rightarrow P\left( {{A_1}} \right) = \frac{{n\left( {{A_1}} \right)}}{{n\left( \Xi \right)}} = \frac{{450}}{{900}} = \frac{1}{2}\)
Có 128 số có 3 chữ số chia hết cho 7 \( \Rightarrow n\left( {{A_2}} \right) = 128 \Rightarrow P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{128}}{{900}} = \frac{{32}}{{225}}\)
Có 64 số có 3 chữ số chia hết cho 14
\( \Rightarrow n\left( {{A_1}{A_2}} \right) = 64 \Rightarrow P\left( {{A_1}{A_2}} \right) = \frac{{n\left( {{A_1}{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{64}}{{900}} = \frac{{16}}{{225}}\)
\( \Rightarrow P\left( A \right) = P\left( {{A_1} \cup {A_2}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) - P\left( {{A_1}{A_2}} \right) = \frac{1}{2} + \frac{{32}}{{225}} - \frac{{16}}{{225}} = \frac{{257}}{{450}}\)
Gọi \({B_1}\) là biến cố: “Số được chọn có 3 chữ số chẵn”, \({B_2}\) là biến cố “Số được chọn có 1 chữ số chẵn và 2 chữ số lẻ”.
Vậy \(B = {B_1} \cup {B_2}\) là biến cố “Số được chọn có tổng các chữ số là số chẵn”.
Có \(4.5.5 = 100\) số có 3 chữ số chẵn \( \Rightarrow n\left( {{B_1}} \right) = 100 \Rightarrow P\left( {{B_1}} \right) = \frac{{n\left( {{B_1}} \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{900}} = \frac{1}{9}\)
Có \(4.5.5 = 100\) số có 3 chữ số có chữ số hàng trăm chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng chục chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng đơn vị chẵn, 2 chữ số còn lại lẻ.
\( \Rightarrow n\left( {{B_2}} \right) = 100 + 125 + 125 = 350 \Rightarrow P\left( {{B_2}} \right) = \frac{{n\left( {{B_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{900}} = \frac{7}{{18}}\)
Vì \({B_1}\) và \({B_2}\) là hai biến cố xung khắc nên ta có:
\(P\left( B \right) = P\left( {{B_1} \cup {B_2}} \right) = P\left( {{B_1}} \right) + P\left( {{B_2}} \right) = \frac{1}{9} + \frac{7}{{18}} = \frac{1}{2}\)

Chọn A
+ Ta có ![]()
![]()
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà ![]() nên c có 3 cách chọn.
nên c có 3 cách chọn.
Ta có: ![]()
Xác suất cần tìm là: